２．主成分分析
はじめに
主成分分析では、元の複数の変数を、より少ない数の変数（合成変数）で効率よくあらわします。測定されている複数の変数から、より少ない数の合成変数をつくります。
たくさんの顕在変数を少ない合成変数に
顕在変数とは、実際に直接測定できる変数です。たとえば、いくつかの顕在変数を（重みづけながら）足し合わせて新たな変数を作ります。この新たな変数は、直接測定してはいません。これは合成変数です。
たとえば、身長、体重、胸囲、腹囲、頭囲など、からだの特性について複数の測定値があるとします。これらは顕在変数です。これに対して、身体的特徴を示す「 size（大きさ）」に関する合成変数や、「shape（形（太っているか痩せているか））」に関する合成変数などを考えることができるでしょう。
変数と次元
元の変数より数少ない合成変数が必要です。
ここで慣れてもらいたいのが、「変数」という言葉と「次元」という言葉を、ある条件の成り立つ時、同じように使う、ということです。ある条件の成り立つ時は、一つの変数が、一つの次元を成すと考えてください。ただしこの時、一つの変数は他の変数と直交する（90度で交わる）とします。これが「ある条件」です。
主成分分析に使う変数に関しては、「変数」と「次元」は同じように使います。ただし「ある条件（直交する）が成り立っているものとします（本当に成り立っているかどうかは不問です）。30変数から主成分分析で3次元解を採用する場合、30次元の情報を3次元に縮約する、です（ただし、分析後得られる次元は、固有値分解後のもので、分析前の次元（＝元の変数）とは異なります）。
2つの変数は2次元の情報であり、変数1と変数2は直交している（90度で交わる）と考えます。同様に3つの変数だと、変数1と変数2と変数3はいずれも互いに直交している、3次元を成していると考えます。4つの変数であれば、変数1と変数2と変数3と変数4、いずれも互いに直交している、この4変数は4次元を成していると考えます。
こうなると、4次元以上の次元が普通にでてきます。20次元だったり30次元だったり、このような空間は図でイメージできませんが、とりあえず、理屈としては存在するのだ、と思ってください。
2次元で定義されている空間（平面）でも、ｘ＝ｙが成り立っているとき、これは1次元の情報しか持ちません。（図表1．参照）
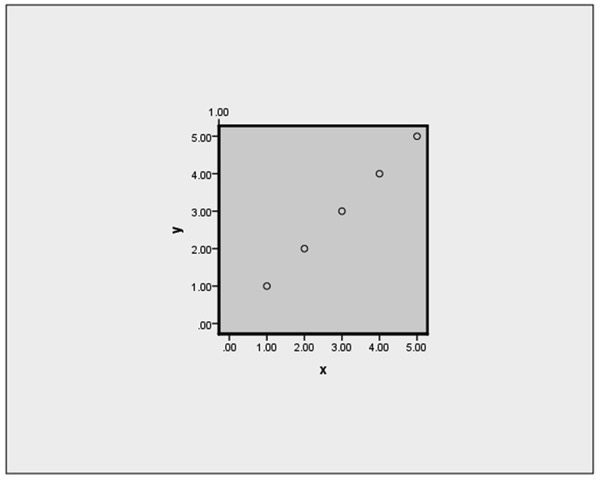図表1．ｘ＝ｙ仮にｘ＝ｙという軸があれば、この軸1つで100％の情報をあらわせます。
3次元で定義されている空間でも、ｘ＝ｙ＝ｚが成り立っているとき、これは1次元の情報しか持ちません。（図表2．参照）
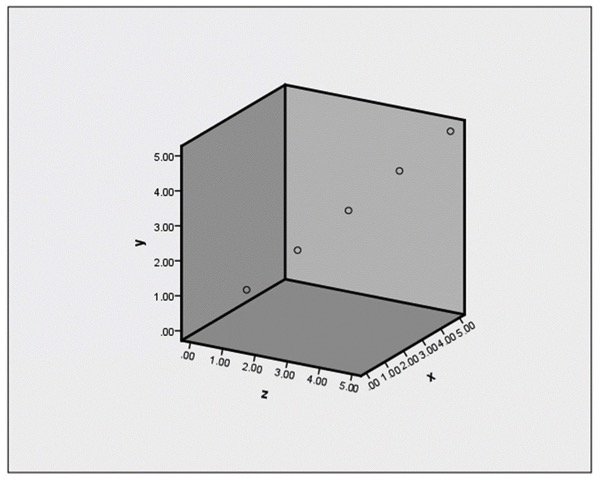図表2．ｘ＝ｙ＝ｚ仮にｘ＝ｙ＝ｚという軸があれば、この軸1つで100％の情報をあらわせます。
ｚまで行ってしまったので、ｘやｙを、ｘ1、ｘ2・・・に変えましょう。
同様に、ｘ1＝ｘ2＝ｘ3＝ｘ4＝ｘ5が成り立っているとき、5つの変数（次元）がありますが、1次元の情報しか持ちません。（もう図は書けません）
次元縮約のイメージ
次元縮約とは、次元を縮めて約す、元の次元数より少ない（縮めた）次元数で、元の情報をできるだけ損なうことなくあらわす（約す）、ということです。たとえば、さきのｘ＝ｙ、ｘ＝ｙ＝ｚ、ｘ1＝ｘ2＝ｘ3＝ｘ4＝ｘ5のようなことです。
分散の大きいところに新しい軸をとおします。たとえば、図表3．を見てください。こう見ると、元の2つの次元（縦軸、横軸）ではなくて、新しい1つの次元上（赤い矢印上）の値だけで、概ねの情報はあらわせそうです。
元の2つの次元（縦軸、横軸）を、より少ない新しい一つの次元（赤い矢印の軸）であらわすようなことが、これ（次元縮約）にあたります。そしてこれが、主成分分析のしていることです。
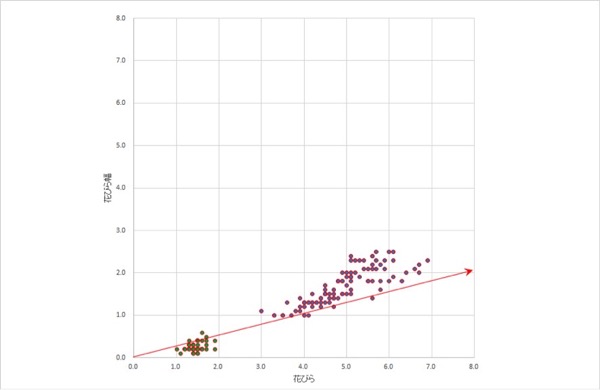図表3．新しい軸を通す（全体）固有値分解
まず1軸目について、最もよく元の情報をあらわすように新しい軸を決めます。2軸目は、元の全情報から、1軸で表現できた情報をすっかり取り除いて、残ったすべての情報を、1軸の場合と同様に、ただし1軸と直交するように（90度で交わるように）決めます。そして3軸も同様、元の情報から、1軸と2軸でもあらわせなかった残りの情報を、最もよくあらわし、しかも1軸、2軸いずれとも直交するように決めます。4軸以降も同様です。元の変数と同じ数まで軸は計算できます（最後のほうは、それ以前までで、元の情報のほぼすべてをあらわしていて、事実上、（ほぼ）0が並ぶだけだったりもしますが）。
こうやって、与えられたデータから、新たに次元を定義して、最もよく元の情報をあらわせるように計算していく手続きが、固有値分解と思ってください。ちょっと先を急ぐと、「相関係数あるいは分散共分散行列の固有値分解」が、主成分分析です。
ところで、図表4．を見ると、原点に近い緑の点と、より原点から離れている青い点と、2種類の点の集まりがあるようにもみえます（ばらついている点自体は図表3と同一です）。であれば、この場合、最もよく元の情報を表す新たな軸を1本とおすより、緑の点について最も情報を良くあらわす新たな軸と、青の点について最もよく情報をあらわす新たな軸の、2本の軸を考えるほうが、実情に沿った軸が得られるようにも思えます（青の線と緑の線は直交していない（90度で交わっていない）ので、実際には簡単な話ではないのですが・・・）（なお、そもそも図表3は、2次元ですべての情報をあらわせています）。
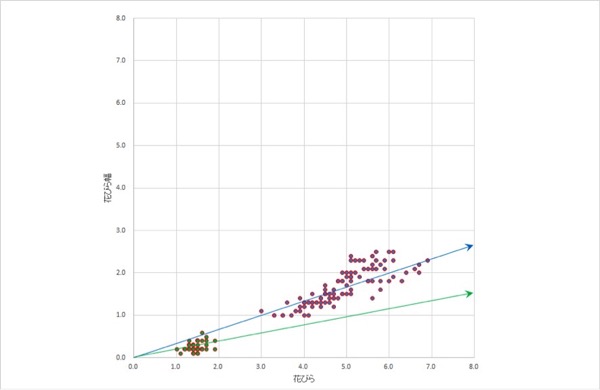図表4．新しい軸を通す（緑の点／青の点）ややイメージ的な（観念的な）話になり脱線しましたが、常に元の情報を最もよくあらわす（図表3．の赤い矢印）ことが最善とは限らないということは、念頭にあっても良いと思います。固有値分解は、こういったことを考えず、とにもかくにも、最もよく情報をあらわす軸を求めます（図表3．の赤い矢印）。
主成分分析の計算手続
あらためて、主成分分析の計算の中身を追ってみます。
「相関係数行列（あるいは分散共分散行列）」を求めます。次に、相関係数行列（分散共分散行列）を「固有値分解」します。固有ベクトルが、そのまま主成分得点です。
これだけです。このシンプルさが、記述的多変量解析のトップに紹介される所以です。多くの場合、主成分得点を使って散布図を描きます（図表5）。
解釈
本連載ではサラっと触れるのみです。手持ちのデータを主成分分析してみた結果の、第1次元×第2次元の結果を掲載します。
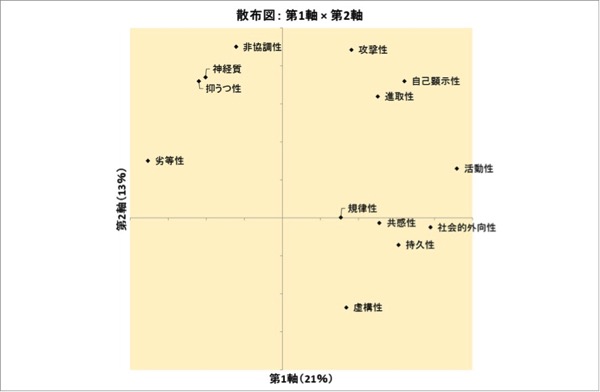図表5．第1次元×第2次元の散布図
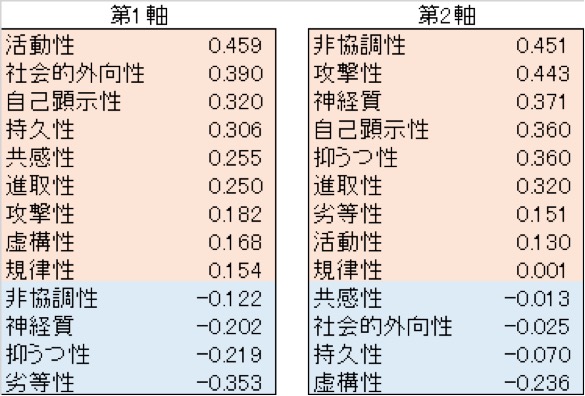図表6．主成分係数（第1次元、第2次元）数値例としては説明率が低い（元の相関行列が持つ情報の34％（21％＋13％）しか再現していない）のですが、公開できるデータということでご容赦を（以降の連載でもこのデータを使って数値例を示します）。
軸を解釈するときは、それぞれ1次元で見ます。図表5の散布図で、第1次元（横軸）を解釈する際は、縦方向の点のばらつきは無視します。つまり、図表6の左、「第1軸」（＝第1次元）の値だけをみて判断します。
ここで、第1次元は、「リーダーシップ」でしょうか。 （＋）方向に「活動性」「社会的外向性」があり、（－）方向に「劣等性」「抑うつ性」があります。
第2次元は、「ひとりよがり」である程度をあらわしているようにも思えます。（＋）方向に「非協調性」「攻撃性」があり、（－）方向に「虚構性」があります（あまり0に近い項目は無視しています）。
さて、ここでは第2次元までしかみませんでした。説明率も低いのに、なぜでしょう。
さきに「固有値分解」の図表3・4で見たように、固有値分解では、とにもかくにも元の情報（分散）を最もよく説明するように軸（次元）を求めます。本当は複数の意味を持つかもしれない点のばらつき（情報）も何もかも考えず、とにかく「元の情報を最もよく説明するように」次元を求めていきます。そして、2次元目以降は、それ以前の次元で説明済の情報は、すべて除いて計算します。
そうすると、低次元では、求めた軸（次元）は、わけのわからないものになっていくことが起こり得ます。
もちろん、第1次元から、きれいにデータに沿った次元の抽出ができる場合もあるでしょう。ただ、確信が持てない場合は、主成分分析では（先の話ですが対応分析でも同様です）、第1次元×第2次元だけ見て、それ以降はあまり注目しないでも良いのかもしれません（こうした状況はマーケティングリサーチなどのアンケートデータなどでしばしば見られます）。これが、2次元までしか見なかった理由です（ちなみにこの数値例は、実は3次元目、4次元目も比較的解釈しやすいのですが・・・）。
