Excelのアドオンの分析ツールを用いて、重回帰分析を行った際に、様々な指標が回帰式の係数とともに出力されます。この記事ではこれらの指標の意味、およびそれらをもとに回帰分析の結果を評価する方法を解説します。
この記事で取り上げられる分析作業の詳細は別の記事で取り上げることにし、今回は評価指標の理解に集中しましょう。
今回の重回帰分析のセットアップ
データの準備
今回、分析対象となるのは、以下のようなデータです。
設定:弁当屋さんは毎日1種類の日替わり弁当を駅から一定距離離れた場所で販売します。一年休日や祝日でも販売します。ポイントカードも運営しており、たまに(特定の曜日や梅雨時期など)ポイント2倍、3倍、5倍などサービスしています。
「生データ」は下図のようとなっています。7つの説明変数 {日付、曜日、天気、平均気温、弁当のカロリー、ポイント倍増の日、販売場所の駅からの距離}、そして説明変数である「売り上げ金額」(単位:万円)から構成されます。期間は2020/6/1から2020/10/30までの152行です。
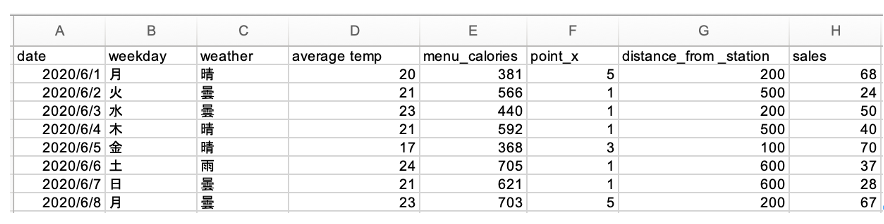
このデータを手に入れた際に、分析の前にまずやらなければいけないことは何だと思いますか?
そうです、weekday(曜日)とweather(天気)を数値に変換することです。コンピュータは数値データしか扱えないので、分析ツールにとりあえず生データのまま突っ込んだら、警告が出てきて、分析を進められなくなります。
そこで、weather(天気)に関しては、One-Hotエンコーディング手法を使ってダミー数値に変換します。3種類の値(晴、曇、雨)のそれぞれに対応する列ができます。
Weekday(曜日)に関しては、天気と同じようにすると7つの列ができて、過学習や共線形性が心配になるので、代わりに”holiday flag” というものを作り、土曜日または日曜日の時のみ1、それ以外は0を入れます。
※このデータ前加工のプロセスは別の記事で示します。
あとは、回帰式の計算には日付型の値がそのままでは使えないので、Excelの関数を使う前に、A列のdateを「数値」型の表現に変換する必要があります。
これでデータの準備が整えられたはずです(下図)。

分析ツールで重回帰分析を行う
これに下図のような分析ツールを用いて、重回帰分析を行いました。
現時点では、最適な説明変数(特徴量)の組み合わせかどうかは不明ですが、いったんは分析の結果をみてみましょう。
重回帰分析の結果を解釈
下図のように重回帰分析の結果が出力されます。これを用いて推定された回帰式の妥当性や精度を評価します。
分析結果の表には様々な指標が表示されており、回帰式の妥当性を正確に評価するためには、各指標の意味を理解する必要があります。回帰式の精度とは、実データにどれくらいよくあてはまるかということです。妥当性とは、各偏回帰係数が統計学の観点から信頼できる値であり、回帰式を予測に使えそうということです。
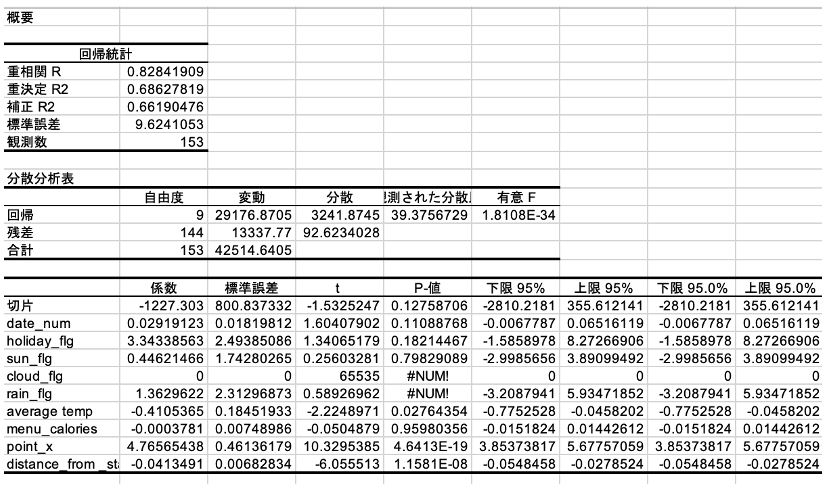
最も重視したい指標は以下となります。
- 回帰式の各係数と切片
- 重決定(R2)と補正R2
- P値とt 値
- 有意F
ここから1つずつ解説していきます。
まず、図の一番上の「回帰統計」表をみましょう。
■重決定 R2
「重決定 R2」は回帰分析における一般に使われる決定係数のことです。「寄与率」とも呼ばれ、回帰分析から得られた回帰式が目的変数の値変動をどの程度説明できているかを表す指標です。別の言葉でいうと、求められた回帰モデルのデータへの当てはまりの良さを示す指標です。0〜1の値を取り、1に近ければ近いほど、データに対する当てはまりが良く、回帰式の精度が高いことを意味しています。表の一番上の「重相関R」はその平方根です。
■補正R2(自由度調整済み決定係数)
「補正R2」は実は重回帰分析で一番重視される指標です。正式には「自由度調整済み決定係数」と呼ばれます。
決定係数(重決定R2)を自由度(標本数 – 説明変数の数)で調整した決定係数と解釈することができます。
1つ前の「普通の決定係数」である重決定R2は、説明変数の個数が多くなればなるほど1に近づく性質があるため、重回帰分析の回帰式の精度を評価する上で限界があります。これに対して、補正R2(自由度調整済決定係数)は、普通の決定係数がデータ数の増加とともに無条件に上昇してしまうことを補正する役割を果たします。
複数の説明変数を使って行う重回帰分析の場合は、説明変数の個数の影響を取り除いた「補正R2」の値を確認しましょう!
■有意F
有意Fは「回帰分析に使用した説明変数の組み合わせに意味はない」という確率を表すものです。この数値が小さければ小さいほど、「偶然の可能性が低い」=「意味のある回帰式を得られた」と解釈することができます。あくまでも目安としてですが、有意Fが0.05または0.01未満であれば、有用な回帰式を得られた可能性が大きいと判断できます。
今回の例では有意Fが10-34 と非常に小さい値になっているので、「回帰分析に使用した説明変数の組み合わせに全く意味がない確率は1%以下である」と言えそうです。
しかし、注意すべきなのは、有意Fから見て組み合わせが「全く偶然ではない」と言えても、現在の説明変数の組み合わせでは有用な回帰式と言えるかは別の問題です。最終的には、重回帰分析では、それぞれの係数のP値(t値)を確認するのが最も重要です。
(※単回帰分析においては有意Fの値はP値が一致します。)
もう少し統計学的な用語を用いて説明すると、「有意F」の数値は「帰無仮説」が採択(観測)される可能性を表しています。説明変数の係数が本当は0である場合の確率の上限に相当します。なぜなら、説明変数の係数が0であれば無意味となり、予測変数が目的変数に影響を及ぼさなくなるからです。改めて、今回の有意Fは非常に小さい値になったので、有意Fだけでみた際に、帰無仮説は棄却してよいと考えられます。これは「回帰係数は0と有意に異なっている」と等価です。
【偏回帰係数とその信頼度】
次に一番下にある、各係数に関する情報をまとめた表を観察しましょう。
- 1列目には各係数の名称(名称が表示されると結果が見やすいので、データ範囲の設定ではヘッダーを含めました。)
- 2列目は分析によって算出された各係数の値であり、3列目はその値の標準誤差(不確定性の幅)
- 4、5列目はt統計量とP値の値
t統計量とP値の統計学的な意味は割愛します。ここでは分析結果の評価の文脈に絞って理解してみましょう。P値をいったん「この係数の分析結果がどれくらい信頼できるものなのかを示している指標」と解釈をしてください。
■P値
Pは「probability(確率)」の頭文字からとってきています。個別の説明変数の1つ1つが目的変数に対して関係があるかどうかを表す指標です。
分析ツールのデフォルトの信頼度設定は95%です。信頼水準はデフォルトの95%を使っていると仮定します。そうすると、P値を100%-95%=5%(0.05)と比べて、算出された係数を「使えるか」どうかを判断します。
一般的にP値が0.05未満であれば、その説明変数は目的変数に対して「関係性がありそう」という判断をします。0.05以上の場合は「関係がなさそう」と捉えることができます。
有意Fが目的変数を説明するための説明変数の組み合わせに意味があるかどうかを表す指標に対し、P値は個別の説明変数が目的変数に対して関係があるかどうかを表します。
■t値
もう気づいている方がいるかもしれませんが、t値はP値の大小と裏返しの関係にあります。t値はP値とセットで観察するとよいです。
P値同様に、t値もそれぞれの説明変数が目的変数に与える影響の大きさを表す指標です。目安として、t値の絶対値が大きければ大きいほど、目的変数に与える影響が強いことを意味しています。逆にt値の絶対値が2より小さい場合は、統計的に判断してその説明変数は目的変数に影響を与えていないと判断します。
P値が小さければ小さいほどt値は大きくなるので、時間がない方はP値の方のみ観察するのもよいでしょう。
■P値の確認と回帰式の評価
それでは、実際に今回の分析結果において、肝心なP値を観察し、「それぞれの説明変数が目的変数に対して関係があるかどうか?」確認します。前述の通り、P値が0.05未より小さければ、その説明変数は目的変数に対して「関係性がありそう」「分析に使えそう」と判断します。
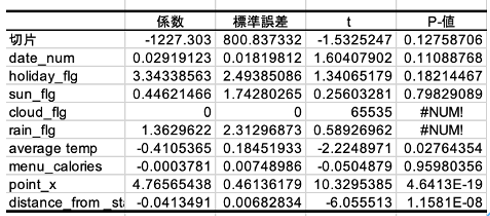
もう一度、注目する部分だけ取り出してみると、P値が評価可能であり、かつ0.05を下回る(あるいはt値の絶対値が2を超える)のは、以下の3つの説明変数です。
- Average_temp(平均気温)
- Point_x (ポイント倍数)
- Distance_from_station(駅からの距離)
評価から分かったこと・分析における次のステップ
上記以外の変数が回帰分析にあまり寄与していないように見える理由として考えられるのは以下です。
- 元から目的変数への影響が少ないまたはほとんどない
- 多重共線性によって、説明変数同士で作用しあって寄与を弱めあっている
この駅の周辺では、平日祝日によらず、お弁当が売れていて、天気にもさほど影響されず、また弁当のカロリーもあまり関係ないようですね。
この分析における次のアクションは、説明変数を再選択した上で、重回帰分析を再度実施し、上記と同じようにその結果を評価することです。
これはExcelを用いた分析や回帰分析に限ったプロセスではありません。どんなデータ分析でも、データの理解、データの前加工、初期分析、評価、試行錯誤の繰り返しが続きます。
今回の分析では具体的に、説明変数を、P値が小さいものに絞ってもう一度重回帰分析を行うことにします。今回は、average_temp、point_x、distance_from_station の3つのみ統計的に有意な回帰係数として使えそうです。
これらを用いた分析は後編で示します。
今回は、分析ツールによって出力された結果の妥当性を解釈することにフォーカスをあてました。
最後に思うことですが…
私は普段PythonやBIツールを使ってデータを処理・分析することが多いです。ビジネスにとってスピード感がよいですが統計学的な理解を見逃しやすいのは事実。
Excelで分析を行う利点の1つは、自動出力される豊富な統計学の指標に意識が集まること。たまに、基本に立ち返ってExcelの分析をやるとリフレッシュしますね。

担当者:ヤン ジャクリン (分析官・講師)

















