アソシエーション分析に使われる指標
アソシエーション分析では、事象Aと事象Bの両方が同時に起こるという「共起頻度」（共起性）に着目しています。共起性は、図1のようなベン図で表すことができます。「共起頻度」は事象Aと事象Bを入れ替えっても変わりません。
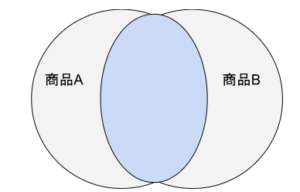図１：共起頻度をVenn図で表現
アソシエーション分析では、共起頻度の他に、より客観的に事象Aと事象Bの関係性を評価するための指標として、主に支持度（Support）、信頼度（Confidence）、リフト値（Lift）の3つを用います。以下では、それぞれの指標の特徴や用途を説明します。
以下の記事では、アソシエーション分析の概要を説明しています。データサイエンティスト検定（DS検定）にもよく出題されるトピックです。
機械学習より前の手法を知る 〜今更聞けないアソシエーション分析
信頼度
信頼度（Confidence）とは、事象Aが発生した状況の下で、事象Bも発生する割合を示す指標です。式1のように表すことができます。
n(A∩B)/n(A) … 式1
ここで、n(A) が 「事象Aが発生したデータの数」、n(A∩B) が「事象Aと事象Bを同時に発生したデータの数」を表します。
信頼度が高い場合、事象Aが発生したときに、高い確率で同時に事象Bも発生していることを意味します。
これを商品に置き換えて考えると、図2のようなイメージとなります。この場合、式1において、n(A) が 「商品Aを購入した顧客の数」、n(A∩B) が「商品Aと商品Bを併せ買いした顧客の数」を表します。そして、信頼度が大きいことは「商品Aが購入された時に、商品Bも併せて購入される確率」が大きいことを意味することになります。
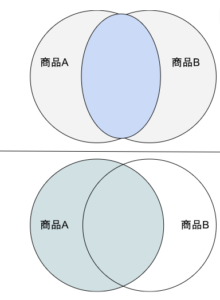図2 ：信頼度の模式図
事象Aと事象Bが同時に発生するケースに着目する意味で、共起頻度と似ているが、共起頻度との違いは、信頼度にはA→Bという方向性があることです。共起頻度はAとBを入れ替えても結果は同じです。一方で式1の信頼度の計算式ではAとBを入れ替えたら事象Aと事象Bの立場が逆転します。
これを具体例で考えましょう。
あるインド料理のレストランにおける注文の履歴から、「辛口のカレーを注文するお客さんは、高い確率でラッシー（ヨーグルトとフルーツなどをブレンドしたインドの甘い飲み物）も注文する」という傾向（アソシエーションルール）が見えたとします。
- 事象A：辛口のカレーを注文する
- 事象B：ラッシーを注文する
辛口カレーを注文したお客さんに口のリフレッシュに良いラッシーを勧めることは良さそうです。しかし、ラッシーを注文したお客さんに辛口カレーを勧めることは適切とは言えません。辛いものが好きではない可能性は大いにあるし、ディナータイムではなく午後のお茶にラッシーを注文しているだけかもしれません。こうして、信頼度を用いて方向性を考慮した2つの事象の関係性を表すことができます。
信頼度の計算例
あるウェブニュースサイトには1日に1000人が訪問した。
A: スポーツカテゴリをみた人が500人。このうち旅行カテゴリもみた人が300人
B: 旅行カテゴリをみた人が50人。このうちグルメカテゴリもみた人が40人
C: グルメカテゴリをみた人が200人。
AとBの信頼度は 250/500 = 0.6
BとCの信頼度は 40/50 = 0.9
したがって、この結果だけを考慮した場合、「旅行カテゴリをみた人がグルメカテゴリもみる確率」は「スポーツカテゴリをみた人が旅行カテゴリもみる確率」より高いと考えることができます。
信頼度の解釈における注意点
次に、信頼度の解釈をしてみましょう。
ごく簡単に捉えるならば、式1で計算された信頼度の数値が大きいほど、「商品Aと商品Bが同時に購入される可能性が大きい」と判断されます。そうすると、一見、商品Aと商品Bのクロスセールスの重要性が高まると考えられます。
確かに、商品同士の関連性をさっと把握したいときに、信頼度という指標は役立ちます。
ただし以下のようなケースには、信頼度の解釈に注意が必要です。
- （ケース１）商品Aの購入者が全体に対して少ないとき
- （ケース２）商品Bは、購入者が非常に多い人気の高い商品であるとき
（ケース1のついて）
商品Aが非常に人気のない商品で、購入者が少ない場合を考えます。この場合、式1の分母が小さく、かつ「たまたま商品Aと商品Bが同時に購入された」ことがおきやすいので、信頼度は見た目上大きくなります。
極端な場合、仮に「商品Aを購入した人が1人だけで、その人がたまたま商品Bを購入した場合」信頼度は100%になります。しかし、この場合、Aを購入した人に商品Bレコメンドすべきとはいえません。
このように、「信頼度がたまたま高い」ケースがあるため、次に解説する「支持度」と一緒に考察を行うべきです。
（ケース２について）
商品Bはほとんどの顧客が購入するような人気商品である場合を考えます。例えば、100人いれば、そのうち90人が商品Bを買うとすると、商品Aを購入した人はかなり高い確率で商品Bも買っていることがお分かりですよね。しかしこの場合、計算上の信頼度の値が高くても、商品Aと商品Bの併売の傾向があるとはいえません。なぜなら、信頼度の値は、商品Bの人気に数字が引っ張られているだけなのですから。
上記のような状況でも、両商品の関係性を正しく判断するためには、後ほど説明する「リフト値」を使います。簡単にいうと、「リフト値」は、ある商品Aの購入が別の商品Bの購入率をどの程度持ちあげるか（リフトするか）をより正確に評価するために用いられます。
支持度
支持度（Support）とは、全てのデータの中で、「事象Aと事象Bが同時に発生するデータ」の割合を示す指標です。
式1のように表されます。
n(A∩B)/n(U) …式2
ここで、n(U) が 「全データの数」、n(AB) が「事象Aと事象Bを同時に発生したデータの数」を表します。
商品Aと商品Bの関係性で考えると、支持度は、全購入者のうち「商品Aと商品Bを同時に購入した顧客数の割合」を示す指標です。式2で計算された支持度の数値が大きいほど、「商品Aと商品Bの組み合わせ」が売上に与える影響が大きいことを示唆しています。
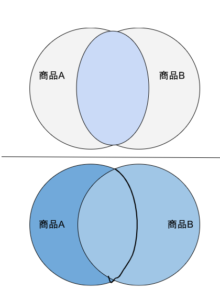図3：支持度の模式図
支持度と信頼度を同時に検討
支持度は信頼度の検証に使用することができます。
式1にある信頼度の計算式をもう一度みてみましょう。
前節で提起したとおり、信頼度だけでは正しい判断ができないようなシナリオが考えられます。そのうちの1つが、「商品Aが非常に人気のない商品で、購入者が少ない場合」です。この時、信頼度が高くても、支持度が低いので、商品Aを購入した人に商品Bをレコメンドする意味があるとはいえません。
実は経験的に、商品Aと商品Bを購入した顧客の絶対数が少なければ、信頼度は高まる傾向にあることが知られています。
まとめると、信頼度を計算してその値が高くても、信頼度だけで判断すると、本来は関連性が高くない商品同士を、誤って関連性が高いと判断してしまうリスクがあります。信頼度を支持度と組み合わせて判断することで、アソシエーション分析の信頼性が高まります。
支持度の計算例
あるウェブニュースサイトには1日に1000人が訪問した。
A: スポーツカテゴリをみた人が500人。このうち旅行カテゴリもみた人が300人
B: 旅行カテゴリをみた人が50人。このうちグルメカテゴリもみた人が40人
C: グルメカテゴリをみた人が200人。
AとBの支持度は 300/1000 = 0.3 （信頼度は 250/500 = 0.6）
BとCの支持度は 40/1000 = 0.04（信頼度は 40/50 = 0.9）
このように、BとCの信頼度が0.9と非常に高くても、支持度が低いことがわかります。これはBの閲覧者がそもそも少なく、旅行カテゴリがあまり人気なさそうであることが関係しています。一方で「AとBの支持度」は「BとCの支持度」よりもはるかに高いです。これはAの閲覧者の数が少なくはないことも寄与してます。このウェブニュースのサイトにおいては、比較的に「Aを見た人にBを推薦する」意味があると考えることができます。
したがって、この結果だけを考慮した場合、「旅行カテゴリをみた人がグルメカテゴリもみる確率」は「スポーツカテゴリをみた人が旅行カテゴリもみる確率」より高いと考えることができます。
信頼度と支持度どちらも高い場合
ちなみに、信頼度と支持度どちらも高い場合はどうでしょうか。
以下の場合を考えましょう。
あるウェブニュースサイトには1日に1000人が訪問した。スポーツカテゴリ（A）をみた人が900人。このうち旅行カテゴリ（B）もみた人が800人
この場合、以下の計算が示すように、AとBの信頼度も支持度も高いです。
AとBの信頼度は 800/900 = 0.88…
AとBの支持度は 800/1000 = 0.80
そして、これらの数値から皆さんが直感的にわかることは、「いずれにしても、大半の顧客が商品Aも商品Bも購入している」ことです。ゆえに、この場合は商品Aと商品Bの率先したクロスセル施策は、マーケティング上そこまで重要ではないと判断することができます。
リフト値
リフト値（Lift）は、事象Aが事象Bをどの程度引き上げる効果があるのかを評価するための指標であり、式3で表すことができます。
{n(A∩B)/n(A)} / {n(B)/n(U)} …式3
式3の分子{n(A∩B)/n(A)} は信頼度（式1）で、分母 {n(B)/n(U)} は全事象数に占める事象Bの割合です。
リフト値が高いのは、式3の分子が比較的大きく、分母が比較的小さい時です。これが意味することを考えてみましょう。
- 分子が大きいということは、事象Aが起きる時に高い確率で事象Aと事象Bが同時に起きていることです。…(1)
- 分母が小さいということは、事象Bの割合がそもそも大きくはないということです。…(2)
(2)が小さいのに、(1)がそれなりに大きいということは、「事象Aが発生することで事象Bの発生率を引き上げている（リフトしている）効果」が見られると解釈します。
これを商品に置き換えて考えてみましょう（図4）。「商品Aが購入された時に、商品Bも併せて購入される確率（信頼度）」（式3の分子）が、「全データにおける、商品Bを購入した顧客の割合」（式3の分母）に比べてどの程度多いかを表します。つまり、商品Aが商品Bの購入率をどの程度上げているのかを表す指標になります。
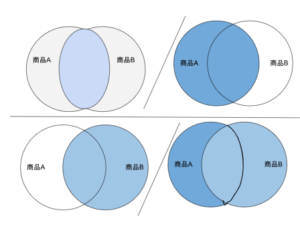図4：リフト値の模式図
リフト値の計算例
あるウェブニュースサイトには1日に1000人が訪問した。
A: スポーツカテゴリをみた人が500人。このうち旅行カテゴリもみた人が300人
B: 旅行カテゴリをみた人が50人。
AとBのリフト値を計算してみましょう。
まずAとBの信頼度を計算すると、{n(A∩B)/n(A)} = 250/500 = 0.6 （リフト値の計算式の分子）
次に {n(B)/n(U)} = 50/1000 = 0.05 （リフト値の計算式の分母）
従って、リスト値は 0.6/0.05 = 12
リフト値の解釈
リフト値が高ければ、商品Bが単体で購入される割合よりも、商品Aと商品Bが同時に購入される割合の方が高いと考えることができます。
また、リフト値が高い場合、商品Aと商品Bをセットで売ることで、商品Bの売り上げをブーストできることが期待できます。
逆に、リフト値が低い時、商品Bはもともとよく売れていて、(A∩B))のような事象が起きても、偶然性が高いです。この場合商品Aと商品Bを一緒にして売ることは適切な戦略とは言えません。
リフト値が低い場合、「商品Bが単独でも十分に購入されている」ことを意味します。この場合、たとえ信頼度が「たまたま」高い値を示しても（例えば商品Aの人気が低い場合）、商品Aと商品Bの繋がりは小さいと判断します。
アソシエーション分析では、信頼度と支持度だけではなく、リフト値を参考にして、「意味のある関係性」と「偶発的な事象」を切り分けることが多いです。
最後に
マーケティング分析において、本当は購買数だけではなく、購入者の属性などの情報も併せて分析に使いたいところです。しかし購入者の属性が手に入らない場合、購入した商品の組み合わせの傾向によってある程度は購買行動の傾向をつかむことができるのがアソシエーション分析です。人間の直感だけでは把握し切れない、意外な買物の組み合わせを可視化する効果も期待できます。
この時に、「関連性が高い」だけでは施策の参考として不十分です。関連性の「方向性」および商品全体の売れ行きに気をつける必要があります。支持度（式2）には方向性がないが、信頼度（式1）とリフト値（式3）に関しては、商品Aと商品Bの間に方向性が定まっています。
また、上記で出した具体例のとおり、「販売個数が少ない人気の低い商品」を対象にしても、アソシエーション分析の結果の誤解釈になりやすく信頼性が低下します。従って、アソシエーション分析はこのような商品には向かないといえます。
