こんにちは!
新卒2年目分析官のMです。
皆さんは風向や波向などの角度で表現することができるデータ(以下角度データ)を扱った経験はありますか?
角度データは0°から360°の周期性を持つため、体重や身長などの線形データとは扱い方が異なってきます。
本記事では基本的な統計量として、角度データの平均方向と分散の算出方法についてご紹介します!
・角度データの平均方向
x1,x2,…,xnを線形観測値としたとき、
一般的な算術平均は(x1+x2+…+xn)/nで与えられます。
しかし角度データの場合、この計算方法では平均方向を算出することはできません。
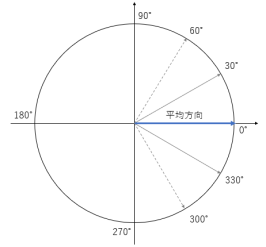
例としてθ1=30°,θ2=330°を角度観測値とした場合で考えてみましょう。
この場合、下図の通り平均方向は0°ですが一般的な算術平均の算出方法だと
(30+330)/2=180°となってしまいます。
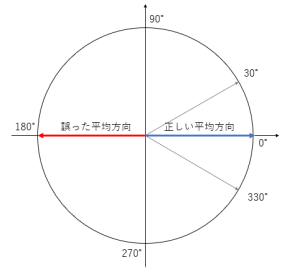
角度データの平均方向を算出するには、
まずはじめに角度観測値θi(i=1,2,…,n)を平面上の単位ベクトルvi=(cosθi,sinθi)に変換します。
つぎに各単位ベクトルviの和を取り、合成ベクトル(C,S)を算出します。
※CとSは以下のように定義されます。
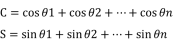
この合成ベクトルの向きが平均方向となります。
先ほどの例だと、
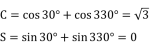
となり、下図の通り合成ベクトルは(√3,0)となります。

よって平均方向は0°となります。
・角度データの分散
平均方向と同様、分散の算出方法も線形データの場合とは異なります。
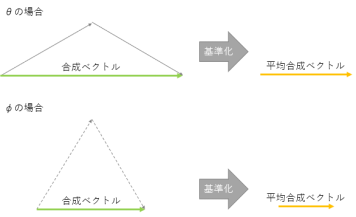
例としてθ1=30°,θ2=330°とφ1=60°,φ2=300°を角度観測値とした場合で考えてみましょう。
θの平均方向とφの平均方向はともに0°となります。
しかし、同じ平均方向をとるθとφでもθの方が散らばり具合が小さく、
より平均方向にデータが集中しています。
この散らばり具合は合成ベクトルを基準化した
平均合成ベクトル(C’,S’)の長さR’(以下平均合成ベクトル長)により数値化することができます。
※C’,S’,R’は以下のように定義されます
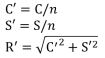
R’は0から1までの値をとり、
1に近いほどデータの散らばり具合は小さく、
また、0に近いほどデータの散らばり具合は大きくなるといえます。
このことから、角度データの分散は1-R’で与えられます。
先ほどの例だと
θの平均合成ベクトル長は√3/2となり、
φの平均合成ベクトル長は1/2となるため、
θのほうが散らばり具合が小さいということになります。
・さいごに
角度データを扱う統計学は方向統計学や角度統計学と呼ばれており、
様々な角度データ用の確率分布や回帰モデル等が存在します。
興味を持たれた方はぜひ調べてみてください!