こんにちは!
データサイエンティストの望月です。
以前、別記事にてベイジアンABテストをご紹介しましたが、
その際、事前分布の設定についてあまり触れていなかったので、
本記事ではその点をもう少し掘り下げていきたいと思います。
事前分布とは?
前回の記事同様、メール配信施策の効果検証を例に話を進めていきます。
ベイジアンABテストを実施するには、あらかじめメールを送ったグループと送らなかったグループそれぞれで、
CV率がだいたいこれぐらいの値を取りうるだろうという予想を立てる必要があります。
これが”事前分布を設定する”ということになります。
CV率のような比率の差を検証したい場合は後々の計算上の都合からベータ分布を指定するのが一般的です。
※客単価のような平均の差を検証したい場合は正規逆ガンマ分布を指定するのが一般的のようです。
ベータ分布の特徴
ベータ分布は下図の通り2つのパラメータαとβをどのような値にするかによって形が変動します。
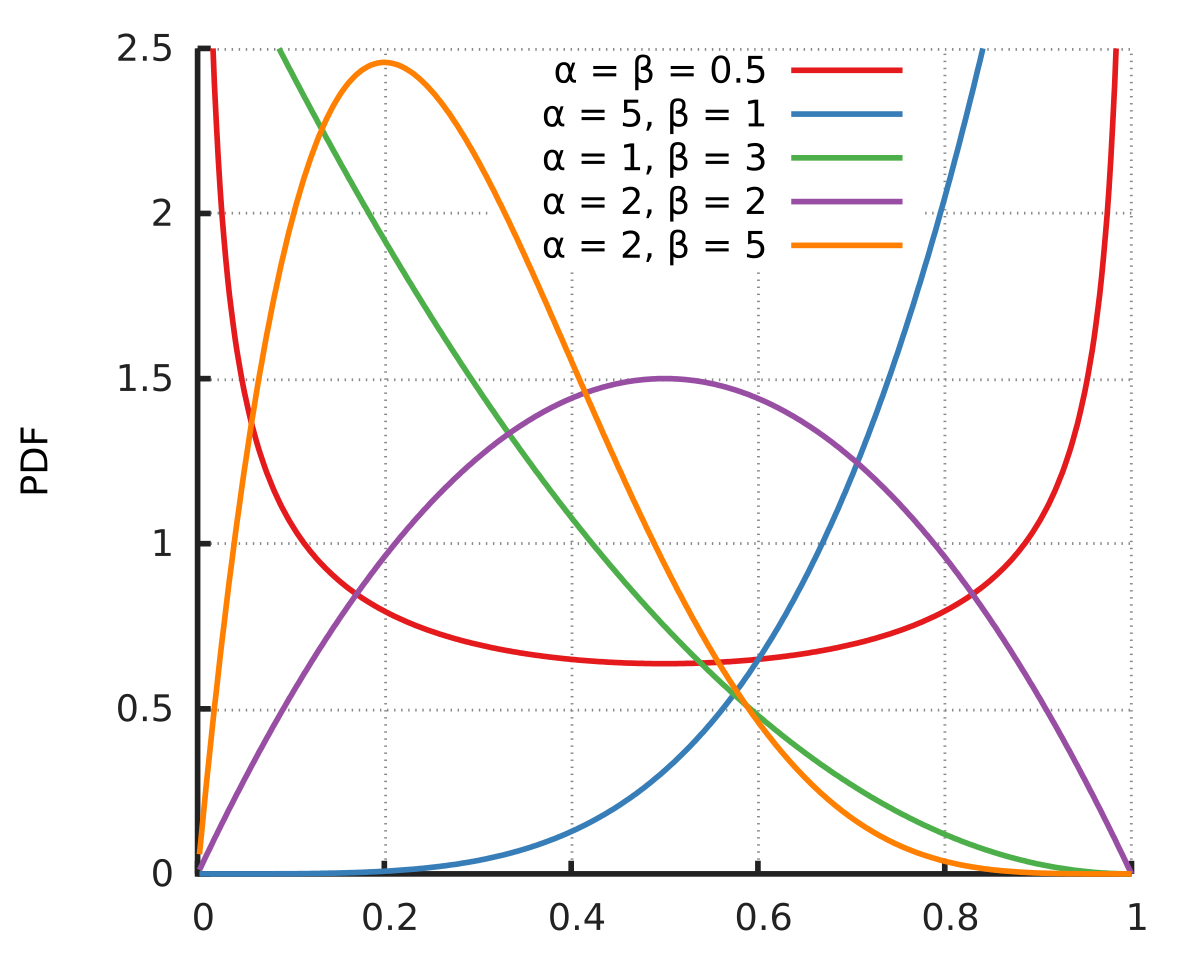
α,β=1の時は[0,1]区間でフラットな一様分布となります。
CV率に関して事前に情報がない・事前分布を設定するにあたって根拠がない場合などは一様分布を事前分布にするケースが多いです。
CV率に関して今までの経験則からある程度目途が立っている場合はα,β=1以外の数値を設定することもあります。
例えばCV率はだいたい40%ということが分かっているとします。
ベータ分布の期待値はα/α+βとなるため、α=2, β=3のベータ分布を事前分布にすることが候補に上がります。
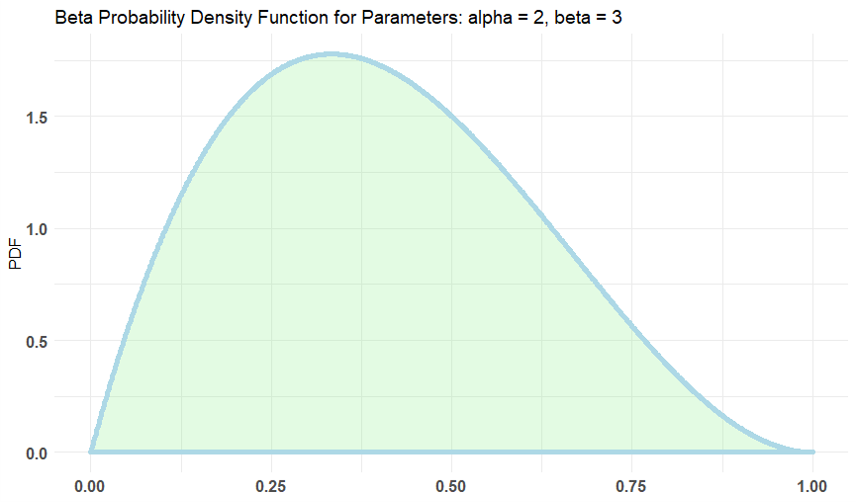
α=20, β=30でも期待値は0.4になりますが、後者のほうが0.4の近くに分布が集中しています。
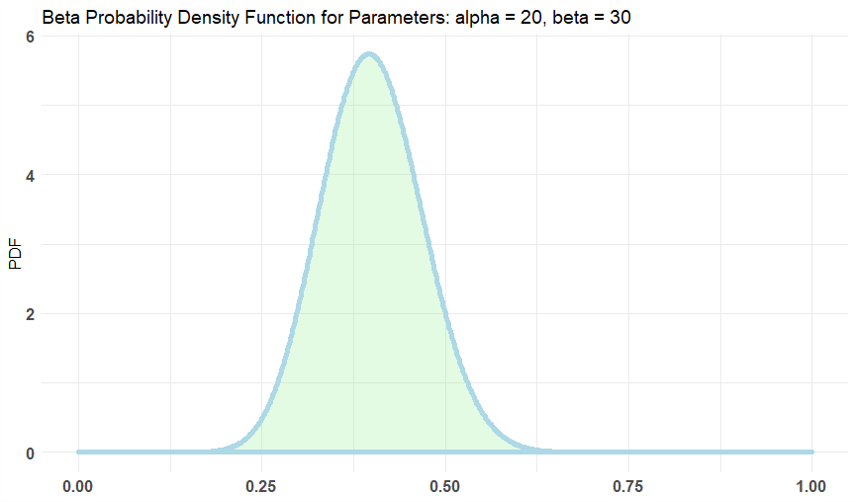
つまり同じ期待値になるようにαとβを設定した場合でもα+βの値が大きいほうがCV率に対して強い仮定を置いていることになります。
Rで確認してみる
仮にメール配信施策の途中結果が下図の通りになったとします。
| CVした | CVしなかった | |
|---|---|---|
| A(メールを送ったグループ) | 85 | 115 |
| B(メールを送らなかったグループ) | 80 | 120 |
今回は下記3パターンのパラメータ設定ごとに結果がどのように変わるか見てみます。
- α,β=1
- α=2, β=3
- α=20, β=30
下図はその結果です。
※上から1.→2.→3.の結果
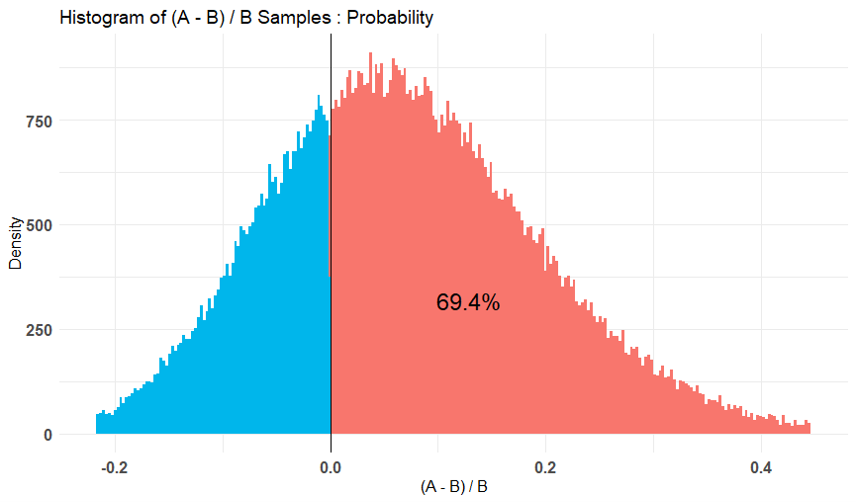
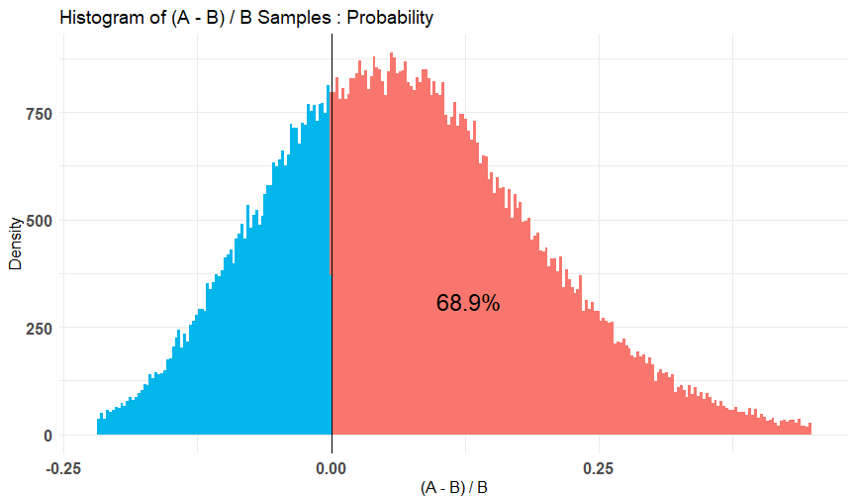
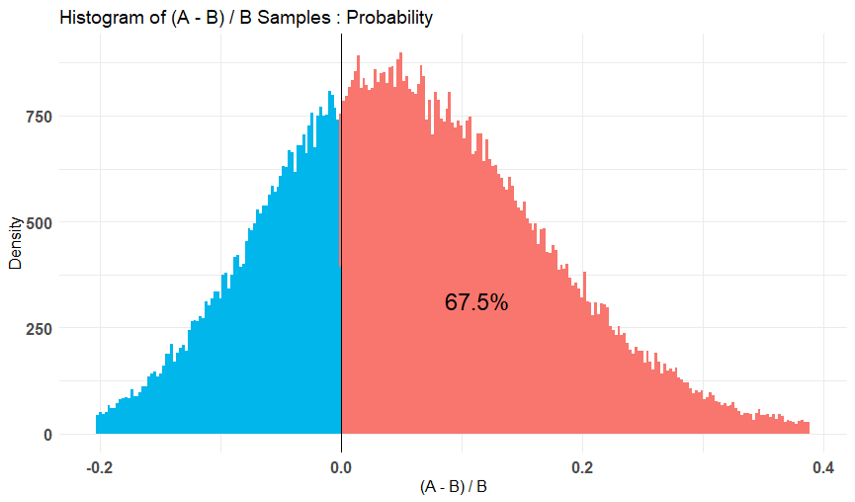
ヒストグラム上に”AはBと比べて何%の確率で効果があると言える”といった数値が表示されており、
1.よりも2.、2.よりも3.の方がこの数値が小さくなっていることが分かります。
これは”CV率はだいたい40%”という仮定を強くしたため、相応のサンプル数がないと効果があると言いにくくなったことを意味しています。
さいごに
どのようなパラメータを設定するかは、結局は分析者次第なのですが、自分はα,β=1でとりあえず試してみるというケースが多いです。
みなさんはどのように設定していますでしょうか?