データには必ずばらつきが伴い、統計学は、ばらつきのあるデータを処理することを得意とします。
この記事では、データのばらつきに関連する指標として、以下の３種類の解釈を比較していこうと思います。
- 標本誤差
- 標準誤差
- 標準偏差
標本誤差と標準誤差
推計統計学において、母集団から標本を抽出して調査を実施し、母集団の性質を推定します。標本データは母集団の部分集合であり、母集団について考える材料に過ぎません。信頼性のある推定結果を得るためには、抽出した標本（サンプル）が偏っていなく、母集団の性質をうまく代表していることが望ましいです。
推定量と実際の母集団の統計量の間にはある程度の誤差が存在します。この誤差は「標本誤差」と呼ばれ、サンプルサイズに依存します。一般的に、抽出されたサンプルのサイズが大きいほど、あるいは母集団のデータのばらつきが小さいほど標本誤差が小さくなります。
しかし、ほとんどの場合、母集団の真の値がわかっていないため、標本誤差を厳密に評価することが不可能です。代わりに、標本誤差のおおよその範囲を判断するために別の指標である「標準誤差（Standard Error）」を使います。
標準誤差とは、標本と母集団の間にどの程度の誤差があるかを確率的に計算した量です。これも小さければ小さいほど標本の調査結果は母集団に近いと言えます。標準誤差は式１のように計算されます。ここで、nはサンプルサイズ、σは母集団の標準偏差です。ちなみに、母集団の標準偏差もまた、知られていない場合は、近似的に標本の不偏標準偏差が使われ、「標準偏差/ sqrt(n)」として計算されます。
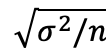式１ 標準誤差の計算式
つまり、標準誤差とは、推定量のバラツキ（精度）を、推定量の標準偏差として表したものとみなすことができます。標準誤差が大きい程、推定量の精度が悪く、標準誤差が小さい程、推定量の精度が良いと解釈します。
また、標準誤差は標本平均の誤差範囲も表しています。例えば、グラフに書くエラーバーは標本誤差の値を使います。
標準偏差とは
平均値や中央値などの基本統計量は、データ分布の中心を表すことができますが、それらだけでは、データ全体の性質をうまく表せないことがあります。平均値と中央値の両方が同じでもデータの分布が異なることもあります。
データのばらつきや広がりを表す基本統計量として「分散」や「標準偏差」が使われます。
標本がn個のデータから成る場合の分散は式2のように計算されます。x_barは標本全体から求められた平均値です。
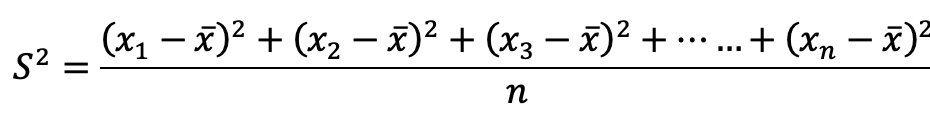式2：分散の計算式
各データ値と平均値の差を変さと呼ばれます。ところが、各データの偏差、つまり「各データ値と平均の差」を全てのデータについて足し合わせると０になってしまいます。これだと使い道がなくなるので、有用な指標として、偏差の２乗を足し合わせて、さらにデータの個数で割った値を使います。この値を分散と呼びます。ちなみに、データの個数（n）で割り算しなかった場合、本来データのばらつきの参考にするはずの指標がデータの個数に従いどんどん大きくなってしまいます。
ところで、分散は元のデータ（と平均の差）を２乗した量を使っているので、単位が元のデータと異なります。一方で、「ばらつき」は元のデータと同じ単位であることが必要です。そこで、分散の平方根をとれば単位を統一できます。これが「標準偏差」であり、本当にデータのばらつきを表すのにふさわしい指標です。
標準偏差は、式3のように分散の平方根をとった量です。
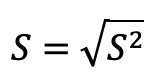式： 標準偏差の計算式（分散の平方根）
標準偏差には次のような特徴があります。
- 平均に近いデータが多い → データのばらつきが小さい→標準偏差が小さい
- 平均から離れたデータが多い →データのばらつきが大きい→標準偏差が大きい
標準偏差が０となるデータは、全てのデータが同じ値であるデータです。
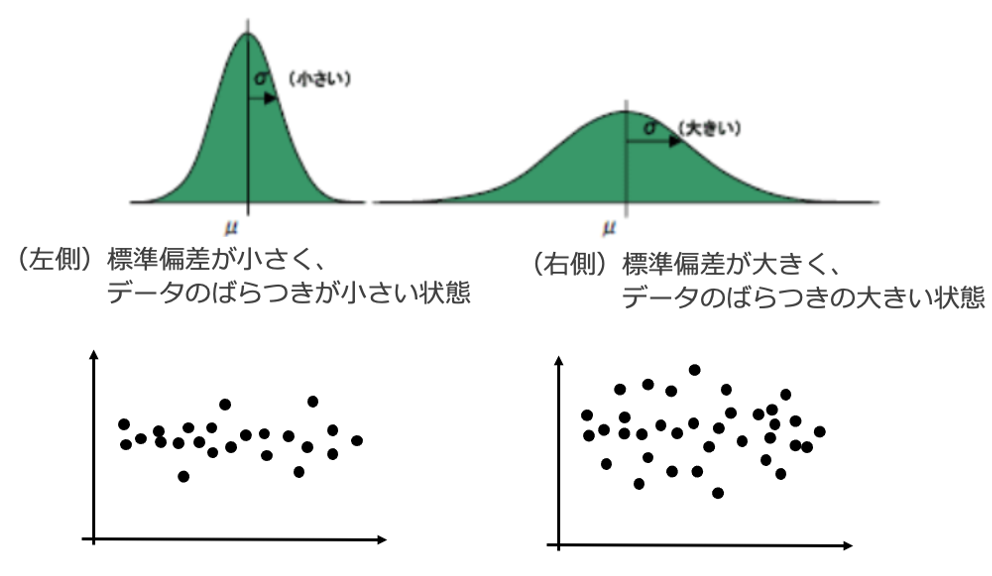
標準誤差と標準偏差の解釈の違い
標準偏差（Standard Deviation）とは、データそのもののばらつきを表す基本統計量です。これに対して、標準誤差（Standard Error）は先述の通り、「推定量の標準偏差」、つまり「推定の精度」を表します。
その使い分けを簡潔にまとめると、以下の表のようになります。
| 用途 | |
| 標準偏差 | データのばらつきを知りたい、比べたい |
| 標準誤差 | 母集団の性質の推定精度 |
標準誤差の計算法は式１のようになり、分母にサンプルサイズがあるため、例えば、アンケート調査を行い、その結果に推測統計学を適用する際に、目的の精度に合わせて、サンプルサイズを決定できます。例えば、推測統計学を用いて、テレビ番組の視聴率を推定するケースでは、調査対象世帯が多い（サンプルサイズnが大きい）ほど、データの回収、整理、計算が大変ではあるが、標準誤差が小さくなり、推定結果の信頼性が上がります。
また、標準誤差の計算式の分子にσ（標本の標準偏差）があるため、もとのデータのばらつきが大きいほど、推定の精度が低くなることがわかります。
