統計検定準1級では、「ベータ関数」や「ガンマ関数」について、出題されることがあります。ベータ関数(β関数)あるいはベータ分布は、正規分布やポアソン分布などに比べて、多くの方にとって馴染みの少ないものかと思います。実際は、工学、物理学の他に、数学や統計学、データサイエンスといった分野でも重要な役割を果たしています。ちなみに、物理学や工学の一部の領域、例えば量子力学や流体力学の一部の計算ではベータ関数が利用されます。
以下、データサイエンスの分野で、ベータ関数がどのように使われるかについて説明します。最初は数式を使わずに、「ベータ関数はこのように使われるよ」ということを理解していただけるための解説をします。最後に数学的な表現に触れます。
ベータ分布は統計学で使われている連続型の確率分布の1つです。成功数aと失敗数bが分かっている試行に関して、成功率 p の分布を表します。ベータ関数はベータ分布の定義に用いられている確率密度関数です。
確率というものは、0と1の間の値をとります。ベータ分布は、2つのパラメータa(成功数)とb(失敗数)を持ち、区間[0,1]で定義されているため、確率や比率を表す確率変数をモデル化するために使用することができます。例えば、コイン投げやクリックスルーレートのような2通りの結果におる現象の「成功確率」をモデル化する際に用いられます。
統計学の中でも、ベイズ統計学でベータ分布がよく使われ、ベイズ推定における事前分布として扱いやすいのが特徴です。ちなみに、ベイズ統計とは「主観確率」を扱う統計学です。ある現象が発生する確率(事前確率)を事前に設定し、その後に新しい情報が得られるたびにその情報を用いて、先ほどの現象が発生する確率を更新し続けます(=事後確率)。このプロセスによって、その事象の真の発生確率「主観確率」を算出します。
A/Bテストは、実世界でのベータ分布の代表的な用途例です。A/Bテストとは、あるウェブサイトの訪問者が機能Aを使う(Aをクリック)確率と機能Bを使う(Bをクリック)確率を比較するものです。ここで、それぞれが選ばれる確率(の不確定性)がベータ分布に従うと仮定し、ウェブサイト訪問者がとる行動をモデル化します。具体的に、各機能のクリック数は、「2通りのどちらの結果になる」ベルヌーイ過程であり、「クリックスルーレートに関する不確定性」をベータ分布で表現しています。
もう1つ、ベータ分布は、”Multi-armed Bandit Problem”(マルチアームバンディット問題)の解決にも使われます。これは、強化学習などにおいて、限られた試行で最大の報酬を得るための最適な行動の方策を見つける問題です。多数の行動の選択肢(=マルチアーム)があり、それぞれが異なる報酬分布、つまり、未知の成功確率を持ちます。これらの確率はベータ分布でモデル化した上で、トレードオフ関係にある「探索」(アームを見つけるための新たな試行)と「利用」(既知の最適なアームを利用)の間のバランスを最適化します。
他に、ベータ分布は、機械学習のアルゴリズムにおける学習率の調整にも使用されます。
最後に、ベータ関数・ベータ分布を数式でも見てみましょう。
改めて、ベータ分布B(a,b)は、2つのパラメータa,bを持つ連続確率分布です。[0,1]で定義され、パラメータによって様々な形状を取ることができます。以下のような積分で計算することができます。
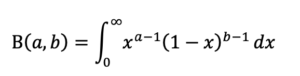
そして、ベータ関数はガンマ関数を用いて、以下のように表すこともできます。
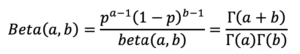
ここで、p確率、aは成功の回数、bは失敗の回数を表します。
そして、上記の式に現れているガンマ関数は以下のような積分で計算することができます。
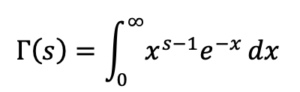
ガンマ関数は階級を一般化したものであり、Γ(s)=(s−1)!が成り立ちます。ここからΓ(s+1)=sΓ(s) という性質を満たすことがわかります。ガンマ関数については別の記事で紹介したいと思います。
以上、普段意識する機会が比較的少ない確率分布の1つであるベータ関数について簡単に紹介しました。
執筆担当:ヤン ジャクリン















