9．決定木
はじめに
全体から始まり、順次（普通は）2分割していきます。幹から葉に木が広がっていくイメージで、全体を細かく分けていきます。
同じような手法
決定木（Decision Trees）には同じような手法が多々あります。交互作用の扱いという点で分けて考えるべきでしょうが、AID（Automatic Interaction Detector：自動交互作用検出器）やその関連手法（CART/C&RT：Classification and Regression Tree）も、データに要求する条件など、手法ごとの特徴もありはしますが、根本的には同じような発想です（CHAID：Chi-squared Automatic Interaction DetectionはAIDです）。基本的に、データを、「全体」から始まって、順次（基本的には）2分割していきます。
ここでは、交互作用を見ない手法を紹介します（ですので、AIDではありません）。
予測か否か
決定木は、予測的側面が強調されることも少なくないようです。これは、過去データから抽出したルールを、新しいデータに当てはめることができるからです。例えば、C5.0などは、予測を念頭に置いているようにも感じます。ですが、本稿では、基本的に、現状の記述、ルールの抽出までに留めて考えることとします。
ここで扱う決定木の特殊性
ここでは、やや特殊な決定木を扱います。が、基本は一緒です。全体（幹）を葉に順次分割していく、ということです。以下、特殊な点です。主に2点。特に1点目が特徴的です。
・一度、分割に使われた予測変数は、それ以降の分割には使用しない。
繰り返し同じ変数が出てくる木は解釈が複雑になるため、このような仕様で説明していきます。木の形成上は正しくないとも言えますが、木の形成に有効な変数を選ぶという観点では、一定程度の有効性はあるであるでしょう。なお、計算結果からは、どの変数が分岐に使われたかは参考になりますが、木の構造自体はあまり深読みしないほうが安全でしょう。
・3分割以上があり得る
予測変数の値は、ここで説明するプログラムでは、一律に順序尺度であると想定して並び替えます（簡便のため）。ただし、変数の分岐数にやや特徴があります。具体的には、隣り合う水準間で繰り返し2群の平均値の差の検定（t検定あるいはWelchの検定）を行い、2水準間で従属変数が有意に違う場合（有意確率は、ここでは20％を指定で行っています）、そこで分岐とするとしました。これを順に隣り合うすべての2水準間で行い分岐を決めています（つまり3分割以上も起こりうる）。
・停止基準
水準間に指定確率より有意となる分岐がない場合も、停止基準に指定したF値を上回る分岐があるあいだは、最もF値が大きくなるように2分岐は行ないます。
最もF値が大きくなるように2分岐しても、停止基準として指定したF値を下回る場合、そこで枝の成長を止めるようにしてあります。
※なお、検定を相当回数繰り返すため、ファミリとしての有意水準を考えると、p値にはほとんど意味はありません。このあたりは、検定など、本稿とはやや異なる分野の考えがベースとして必要かもしれません。以下に参考文献を一冊あげておきます。
永田靖・吉田道弘（1997）統計的多重比較法の基礎．サイエンティスト社
木
まずは一例を見てみましょう。
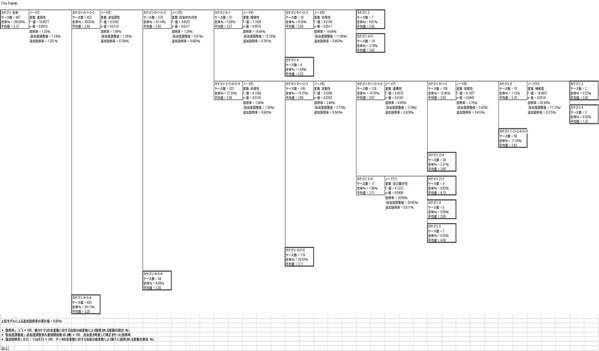
図表1．Tree Diagram（クリックで拡大）一番左、まずは全体です。それが「進取性」で分岐しています。カテゴリが「0」～「3」と「4」～「6」に2分岐しています。そのうち、「0」～「3」のほうが、さらに「非協調性」で分岐しています。ここでも、カテゴリが「0」～「3」であるか、「4」～「6」であるかで分かれます。カテゴリ「0」～「3」のほうは、さらに「社会的外向性」で分岐します。今度は、社会的外向性が「0」～「1」と、「2」～「6」で分かれています。
なお、分岐が終わっている「進取性」の「4」～「6」、「非協調性」の「4」～「6」は、それ以上分岐させるほどの条件を（分岐の条件は分析者が指定します）持たない、ということです。
細かい仕様はいろいろあるのですが、基本的には、いたってシンプルなことをしているだけです。少なくないケースで、この手の手法を予測に使おうとして、指定項目など、いろいろ煩雑になっているケースがあるようですが、現状の記述を行う分には、難しいことはありません。
決定木の計算手続
従属変数はひとつ、必ず指定します。どの変数の値が異なるようにデータを分岐させていくのか、基準となる値です。ここでは「ブラウズ」、インターネット閲覧をする程度を見ています。
例えば、「進取性」が高いとインターネット閲覧の頻度が高く、「進取性」が低いとインターネット閲覧の頻度が低い、などといった場合の、インターネットの閲覧頻度＝「ブラウズ」です。ここでは、これを従属変数として見ています。
全体から始まります。まず、すべての変数でデータを分割してみます。
ある変数にはいくつも選択肢があるでしょう。ここでは、すべての変数で、選択肢は順序尺度だとしています。例えば、「はい」「いいえ」も、「1」「2」という順序尺度だとみなします。
そのうえで、すべての変数で、選択肢を2つ以上に分けます。例えば、2つに分ける場合だと、「1」「2」「3」「4」「5」と選択肢があれば、「1」と「2」「3」「4」「5」で分かれるのか、「1」「2」と「3」「4」「5」で分かれるのか、「1」「2」「3」と「4」「5」で分かれるのか、「1」「2」「3」「4」と「5」で分かれるのか、この場合4通りの可能性があります。仕様上、すべての選択肢は順序尺度だとしています。「1」「3」と「2」「4」「5」というように、順序を無視して分けることはありません。
ただし2分割とは限りません。3つに分かれる場合もあるでしょう。
そこで、「1」「2」「3」「4」「5」すべての隣り合う選択肢間で2群の平均値の差の検定をやってみましょう（従属変数は必ず量的変数だとして考えます）（検定の多重性を考えると、あまりに多数回の検定を繰り返すので、p値には意味は無いと考えてよいでしょう。ただ単に、計算の制御上の数値の指定くらいの意味しかありません）。
その結果（便宜上）有意差ありとなったカテゴリ間でデータを区切ります。そうすると、3分割以上となる場合もあるでしょう（実際、図表1では、ノード11で、「自己顕示性」が3つに分かれました）。
このようにして、すべての変数について、選択肢を2つ以上に分岐させた場合のF値（群内分散に対して群間分散がどれだけあるか）を計算してみます。そのうえで、最もF値が大きくなる変数で、従属変数を分岐させます。
これで、一つ目の分岐変数と、分岐の仕方（変数の分かれる数、分かれ方）が決まります。あとはこれを繰り返していくだけです。ただし、分岐をストップする基準は必要です。
例えば、分割した際の、従属変数のF値が、一定を下回る場合は、もはや分岐不要、分岐させない、木の（その方向への）成長を止める、とします。
こうすると、一定のところで、木の成長は止まります。
解釈
先と同様ですが、改めて下記に書いておきます。図表1と見比べてみてください。
一番左、まずは全体です。回答者の100％。「ブラウズ」の平均値は3.13。
それが、「進取性」で分岐しています。カテゴリが「0」～「3」と「4」～「6」に2分岐しています。
そのうち、「0」～「3」のほうは、さらに「非協調性」で分岐していきます。
「進取性」が「0」～「3」の、「ブラウズ」の値の平均は2.98。全体平均（3.13）よりも低くなっています。
「4」～「6」のほうは、そこで分岐は終わりです。全体の50％ほどはここに含まれます。このとき「ブラウズ」の平均は3.28。全体よりは少し高いようです。
さて、「非協調性」。カテゴリが「0」～「3」か、「4」～「6」かで分かれます。
カテゴリ「0」～「3」のほうは、さらに「社会的外向性」で分岐していきます。このときの「ブラウズ」は2.92。全体平均より低めです。
「4」～「6」のほうは分岐終了。全体の7％ほどはここ。「ブラウズ」は3.38。全体より頻度高くネット閲覧しているようです。
今度は、「社会的外向性」が「0」～「1」と、「2」～「6」で分かれています。
「0」～「1」のほうは、さらに「規律性」で分岐していきます。全体の6％ほど。N（度数）で見ると、51。だいぶ小さくなってきています。「ブラウズ」は、平均3.27。これまで、「進取性」「非協調性」と「ブラウズ」の平均は全体平均より低かったのですが、その中でも、「ブラウズ」の値が高い群のようです。
「2」～「6」のほうは、「共感性」で分岐。全体の37％ほど。N（度数）で見ると320以上。まだある程度の大きさがあります。「ブラウズ」は平均2.86。
・・・こうしてみていくと、「持久性」と「抑うつ性」はこの木に含まれませんでした。「ブラウズ」頻度を分ける働きは示さなかったのでしょう。
また、「自己顕示性」は、それまでに、いくつもの性格的特性での分岐を経て、ようやく効果的な分岐を示したようです。例えば、N=867の最初の分岐の時点での、「自己顕示性」で分岐した場合の、得点別の平均「ブラウズ」得点を見てみましょう（ノード1／N=867の列）（ここでは比較のため、カテゴリ「2」「3」／「4」／「5」ごとに計算（カテゴリ「0」「1」「6」はノード11の分岐で該当対象者数が＜2となり分散の計算が成り立たないため除外された））。
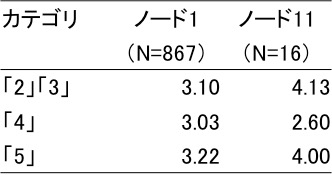図表2．「自己顕示性」の得点別「ブラウズ」平均値Nが極端に違いますが、Nが16まで絞り込まれた段階でようやく、「自己顕示性」の得点ごとに「ブラウズ」の平均点の開きが大きく異なった、という様子がわかります。
