(注意)この記事は2023年3月中に、GPT-3.5のChatGPTに対して質問したものです。
ここではZero-shot promptを使用しており、プロンプトエンジニアリングの工夫を全く施しませんでした。2023年5月に試すと、記事中の「因数分解」など、GPT-4はもちろんGPT-3.5も正しく解くことができました。
先日、こちらの記事で、AIを用いて数学の問題を解くことえお解説しました。

今回は、以下について考えていきたいと思います。
ChatGPTは次に来る単語を予測することが得意、ということがよく知られています。
では、ChatGPTは数学ができるのか?
ChatGPTは次のような中学レベルの問題を解くことができそうです。
Q: x+5=12 をxについて解いてください。

簡単な解法または公式を覚えるだけで解ける問題であれば、そのような問題と解法あたは公式のセットを含む学習データを与えればいいと思われます。
では、上記だけでは不十分な問題をやらせてみましょう。
次は高校で学ぶ因数分解の問題です。因数分解となると、公式に数字を当てはめるだけではなく、何らかの規則を学ぶ必要がありそうです。
Q: x^2+x-2=0 を因数分解してください

上記の課題を解くために、ChatGPTは以下の全てができないといけないです。
- そもそも問題(方程式)を解く、または、展開する、とはどんなことなのかを知る
- 因数分解にはどのようなパターンがあるのかを知って、場合わけで使い分ける
- 判断したパターンに沿って四則演算を行う
- 論理的な説明で解法を説明する
どうして、ここまで出来るのでしょうか?
ChatGPTによる数学力は、以下のように理解することができます。
実際は、数字を操作することそのものは学習していなくて、操作の結果を学んでいます。学習データとして、数学の問題とその回答のセットが多数使われており、ChatGPTは、問題の文章とそれに続く数式における単語と数字の関係性を学習します。つまり、数学としてではなく、文章(テキスト)として学習しています。そうすると、文章における次の単語を予測するのと同様に、次に来る数値を学習し予測できるわけです。
こうして、大量な問題文と数字や計算記号から、「計算のルール」とみなせるものを導き出せたことになります。こうすることで、ChatGPTの内部で、見かけ上、数学と見做せるような抽象的な概念が出来上がります。ただ、記号と記号の関係性に過ぎないので、その記号が有する数学の意味を理解しておらず、いわゆる「シンボル・グラウンディング」問題ですね。
それでは、ChatGPTの学習の限界を試すような、より段階的な思考を必要とする問題を出してみましょう。
Q: 以下の連立方程式を解いてください。
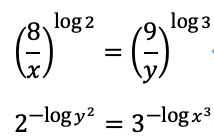

見事に間違いましたね。
ここでは、指数と対数の関係性を活用しようとしていることがわかります。ただし、途中から、理にかなわないような式変形をし、人間ならしないのであろう珍しい間違い方をしています。
実は、ChatGPTがより上手に難しい問題を解かせる秘訣があったのです。
Large Language Models are Zero-Shot Reasoners
以下は印象に残ったポイント
- 発見した呪文は “Let’s think step by step” を質問の最後に加えるだけで、それまで出来なかった複雑な数学の問題も正解できる
- 思考の連鎖を促すフレーズが呪文のポイント(これを超える呪文はその後いくら探してもほとんど見つからない)
- 言語モデルは二重人格を持つ:直感的な思考ネットワークと論理的な思考ネットワーク(論理的な文章と直感的なブログで学習したので)➡︎ 「呪文」は、モデルの挙動を思考的ネットワークにスイッチしてくれた(言語モデルは良くも悪くも特定の言葉に反応するのを利用)
- モデルの規模(パラメータ数)がある閾値を超えないと、呪文は無効(複数の人格を持つための十分な脳の容量)
ちなみに、上記の連立方程式の問題に、”Let’s think step by step” を最後に付け加えても、ほぼ同じ間違いをしました。この呪文が効かないような問題も当然あるでしょう。
より簡単な連立方程式はどうかな、と思って以下を試しました。
Q 以下の連立方程式を解いてください。
x +3y = 1
2x-3y=-2
なんだか、高度そうなコードまで出してくれたが、こんな簡単な方程式も、残念ながら間違えました。
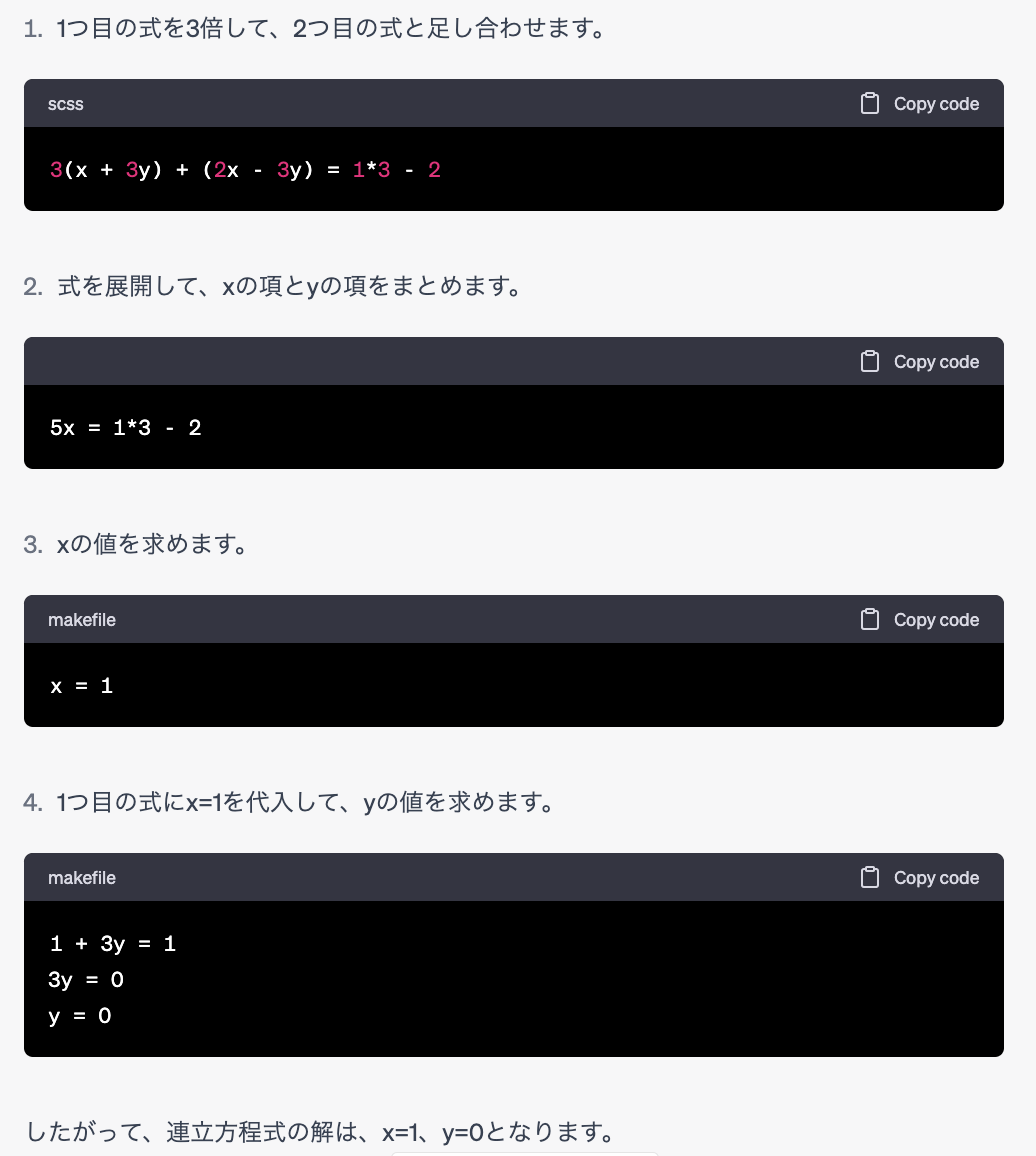
こうして、ChatGPTは自信たっぷりの解法を展開しながら、実は全く間違っているので、上手いウソをつくことがあります。(分からないなら分からないと言って欲しいですよね 笑)。そうすると、自分自身は全く解法の方向性を知らず、解答を読んでも理解できない場合は、ChatGPTを使って数学を解かせても、間違えた回答を見分けられないでしょう。逆に、時方はわかっていて、計算や式展開が難しいだけであれば、ChatGPTを使えるでしょう。
ChatGPTの振る舞いとクセを理解できるためにはだいぶ時間がかかりそうです。
【生成AIに関する記事を読みたい方はこちらから『ChatGPTビジネスレポート』に無料登録してください】
執筆担当:ヤン ジャクリン (データ分析官・講師)


















