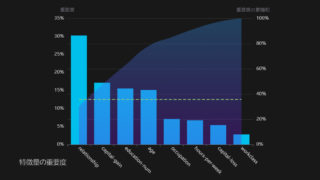
統計検定2級では、回帰分析がよく出ます。
一般的には、最小二乗法を用いて、回帰係数を推定します。推定された係数については、(特に、回帰分析と仮説検定にまたがる出題では)以下が問題を解くのによく使われます。
y=α+βxとして最小二乗法で係数を推定した際に、βの推定値は以下のような正規分布に従う確率変数です。
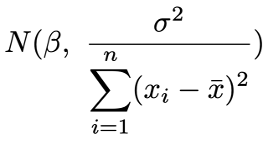
よく使う上記の「お決まり」ですが、「なぜ?」と思いますよね。学生時代に愛用していた東京大学出版会の『統計学入門』(どこが入門ですか???!!笑)を掘り出して、証明がどこかに載っていないかを探したが、曖昧なことしか記載されていませんでした。これはこの本の対象者には「当たり前のことですかね」と考えつつ、自分で証明してみることにしました。
以下、手書きの計算の掲載ですみません。
とはいえ、手書きの補助計算を教材にもよく載せます。PCでものを書く時代、手を動かして計算をする雰囲気を出したいところです。
回帰係数の不偏推定量の分布に関する証明
βの推定値が以下の正規分布に従うことを証明
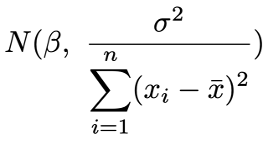
平均は母数に等しいので、ここでは分散が以下になることを示せば良いのです。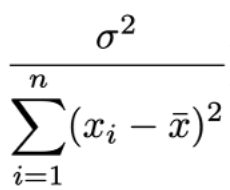
データにはεという誤差項が付くと仮定します。
まず、最小二乗法の解から出発し、βの式変形をひたすらします。
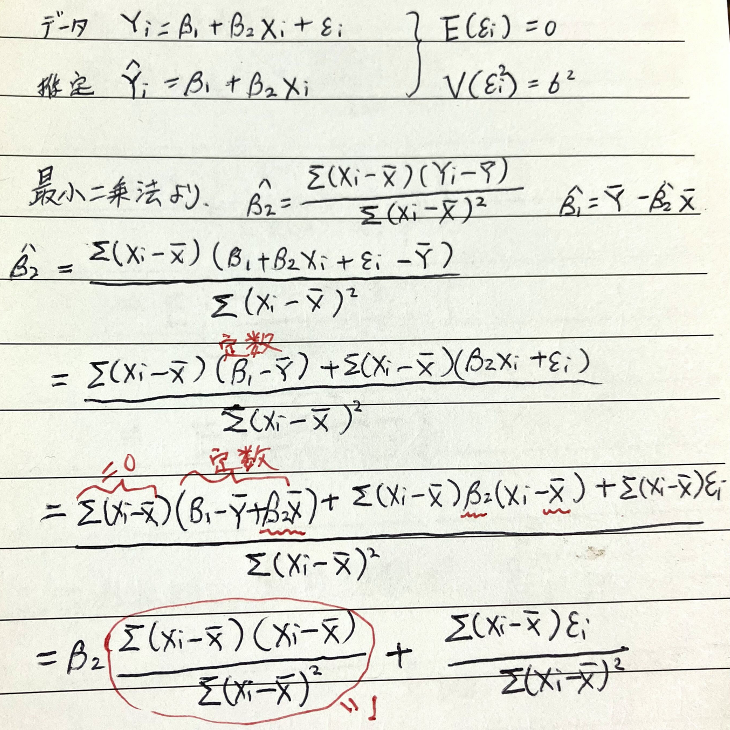
上記の式変形の結果を使って、βの分散を求めます。
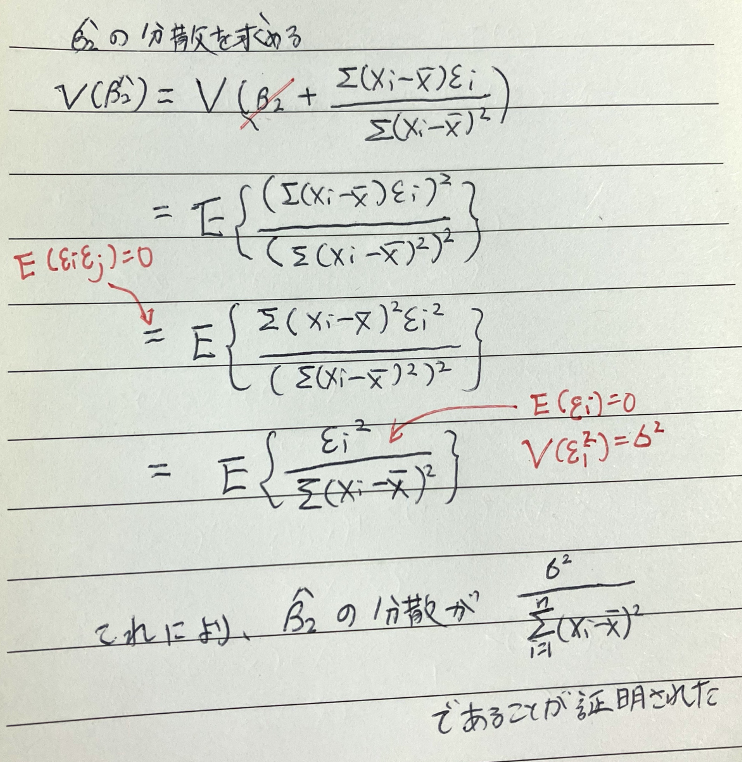
証明は以上となります。
苦労して証明できるようになると、実務で使えそうな場面でその定理を思い出しやすくなります。
執筆担当者:ヤン ジャクリン(データ分析官、講師)