『正規分布を使わずに『仮説検定』の理論を驚くほどわかりやすく〜 Part1〜』では、コイン投げという身近なものを用いて仮説検定について考えていました。以下のようなシナリオです。
コイン投げを行った結果は以下となりました。
- 「コインを5回投げて、裏が5回連続で出た」
- 「コインを10回投げて、裏が10回連続で出た」
この場合、仮説は以下となります。
- 帰無仮説:コインにしかけはない。表が出る確率は0.5である。
- 対立仮説:コインにしかけがある。表が出る確率は0.5ではない。
上記のどちらが妥当か(どちらが「正しいか」ではない!)を検定したいです。
今回は、有意水準(ほとんど起こりえないこととみなす確率の基準)を1%にします。統計検定量を「コインの裏が出た回数」とし、以下のようになります。
- コイン5回の例:コインの裏が出た回数=5
- コイン10回の例:コインの裏が出た回数=10
これで、仮説検定における「標本データに基づいて検定統計量を計算する」の部分が完了です。
ここから、仮説検定のクライマックスに近づきます。
コイン投げの例で仮説を検証しましょう(Part1からの続き)
コインの裏が連続5回出るのはありえない?
まずは、「コインの裏が5回出た」の例を考えてみます。
帰無仮説が正しい場合、すなわち主催者の主張どおり「コインにしかけはなく、表が出る確率は0.5である」場合に、統計検定量「コインの裏が出た回数=5」が、どれくらいの確率で起こりうるのかを計算します。
| 統計検定量 | 確率 | 説明 |
| 0 | 3.125% | 表5回 ⇒ 0.5×0.5×0.5×0.5×0.5=0.03125 |
| 1 | 15.625% | 表4回&裏1回 ⇒ 5C1×0.5×0.5×0.5×0.5×0.5=0.15625 |
| 2 | 31.25% | 表3回&裏2回 ⇒ 5C2×0.5×0.5×0.5×0.5×0.5=0.3125 |
| 3 | 31.25% | 表2回&裏3回 ⇒ 5C3×0.5×0.5×0.5×0.5×0.5=0.3125 |
| 4 | 15.625% | 表1回&裏4回 ⇒ 5C4×0.5×0.5×0.5×0.5×0.5=0.15625 |
| 5 | 3.125% | 裏5回 ⇒ 0.5×0.5×0.5×0.5×0.5=0.03125 |
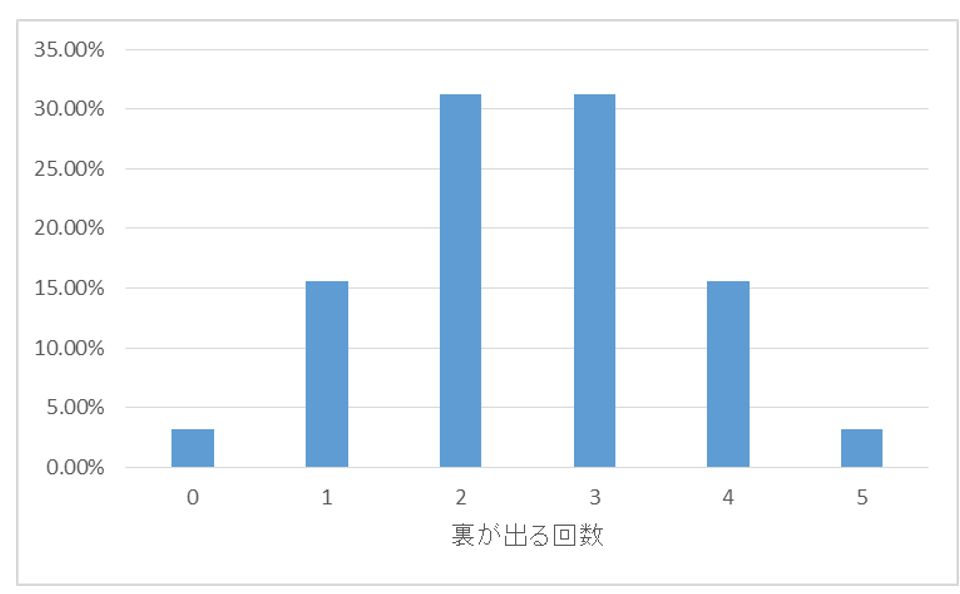
帰無仮説が正しい場合でも、「コインの裏が出た回数=5」という出来事が3.125%の確率で起きうるわけで、有意水準1%を上回っています。よって、事前に定めた基準に従い、「確率ほぼゼロ」とはみなせず、帰無仮説が正しい場合にも十分に起こりうることと判断するわけです。
この「帰無仮説が正しい場合にも十分に起こりうることと判断する」ことを、統計学の用語で「帰無仮説を棄却しない」と表現します[1]。
ここで注意点が1つあります。この仮説検定の結果からは「帰無仮説が間違っているとは言い切れない」「対立仮説が正しいとは言えない」しか言えません。決して、「帰無仮説が証明された」とも「帰無仮説が正しい」とも言えませんし、「対立仮説が間違っていた」と言うこともできません。
つまり、コイン投げの例でいくら5回続けて裏が出たとしても、「インチキだ」と言い切れなかった、ということになります。一方で、「インチキではない」ことが証明されたわけではありませんし、「インチキではない」ことが証明されたわけでもありません。つまりは証拠不十分だったということにすぎません。
以上が、コイン5回の例での仮説検定の結論です。
コインの裏が連続10回出るのはありえない?
続いて、「コインの裏が10回出た」の例を考えます。
帰無仮説が正しい場合、すなわち主催者の主張どおり「コインにしかけはなく、表が出る確率は0.5である」場合に、統計検定量「コインの裏が出た回数=10」が、どれくらいの確率で起こりうるのかを計算します。
| 統計検定量 | 確率 | 説明 |
| 0 | 0.09765625% | 表10回 ⇒ (0.5)10=0.0009765625 |
| 1 | 0.9765625% | 表9回&裏1回 ⇒ 5C1×(0.5)10=0.009765625 |
| 2 | 4.39453125% | 表8回&裏2回 ⇒ 5C2×(0.5)10=0.0439453125 |
| 3 | 11.71875% | 表7回&裏3回 ⇒ 5C3×(0.5)10=0.1171875 |
| 4 | 20.5078125% | 表6回&裏4回 ⇒ 5C4×(0.5)10=0.205078125 |
| 5 | 24.609375% | 表5回&裏5回 ⇒ 5C1×(0.5)10=0.24609375 |
| 6 | 20.5078125% | 表4回&裏6回 ⇒ 5C2×(0.5)10=0.205078125 |
| 7 | 11.71875% | 表3回&裏7回 ⇒ 5C3×(0.5)10=0.1171875 |
| 8 | 4.39453125% | 表2回&裏8回 ⇒ 5C4×(0.5)10=0.0439453125 |
| 9 | 0.9765625% | 表1回&裏9回 ⇒ 5C4×(0.5)10=0.009765625 |
| 10 | 0.09765625% | 裏10回 ⇒ (0.5)10=0.0009765625 |
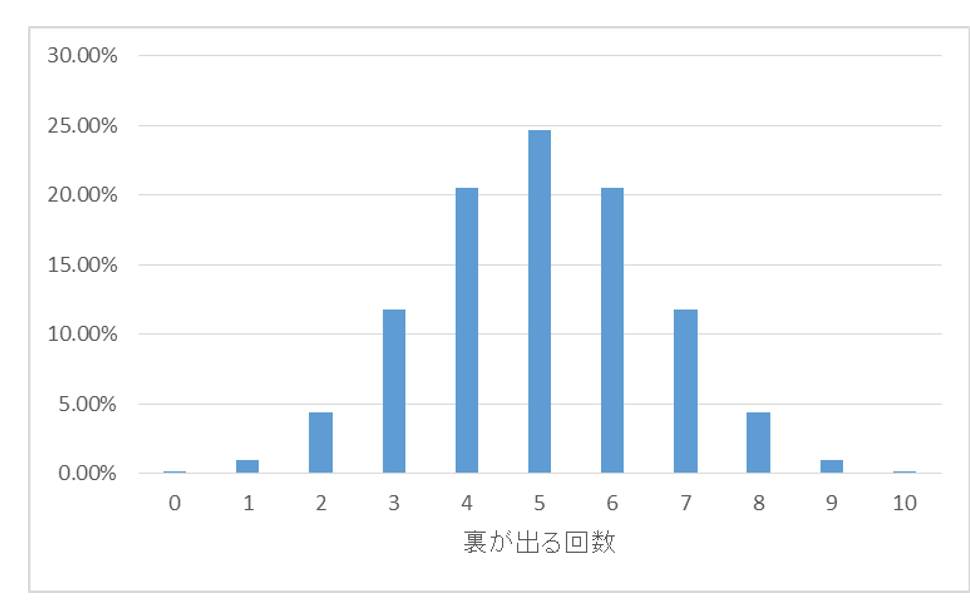
帰無仮説が正しい場合でも、「コインの裏が出た回数=10」という出来事が0.09765625%の確率で起きうるわけですが、有意水準1%を下回っています。よって、事前に定めた基準に従い、「確率ほぼゼロ」とはみなし、帰無仮説が正しい場合には「ほとんど起こりえないこと」であると考えるわけです。すなわち、対立仮説「コインにしかけがある。表が出る確率は0.5ではない」と判断するわけです。
以上をもって、検定(仮説の検証)を行い、その結果をもとに帰無仮説を棄却するかを判断する」ところまで完了したことになります。
帰無仮説と対立仮説に関する誤解を解く
仮説検定の結果に基づく判断が間違っている可能性
コイン5回の例では、コインにしかけがなくても、裏が5回連続出る確率は3.125%あるので、「コインにしかけがあるとは言えない」と判断しました。一方、コイン10回の例では、コインにしかけがないとすると、裏が10回連続出る確率は0.09765625%しかないのだから、「コインにしかけがある」と判断しました。そしてその基準は、有意水準という、検定を行う人が自分で決めた基準でした。
ところが、この判断が間違っている可能性はないのでしょうか?
もちろんあります。
Part1ですでに述べたように、統計学では、100%確実な答えを出すことはできません。確率的な現象を扱う学問ですので、下図のように、帰無仮説と対立仮説の妥当性にはグラデーションがあります。「帰無仮説が妥当」や「対立仮説が妥当」といえる領域だけでなく、「帰無仮説と対立仮説のどちらが妥当ともいえない」領域があります。そして、有意水準は、このグラデーションの中で、仮説検定を行う人が「ここを基準に判断しよう」と設定するのです。
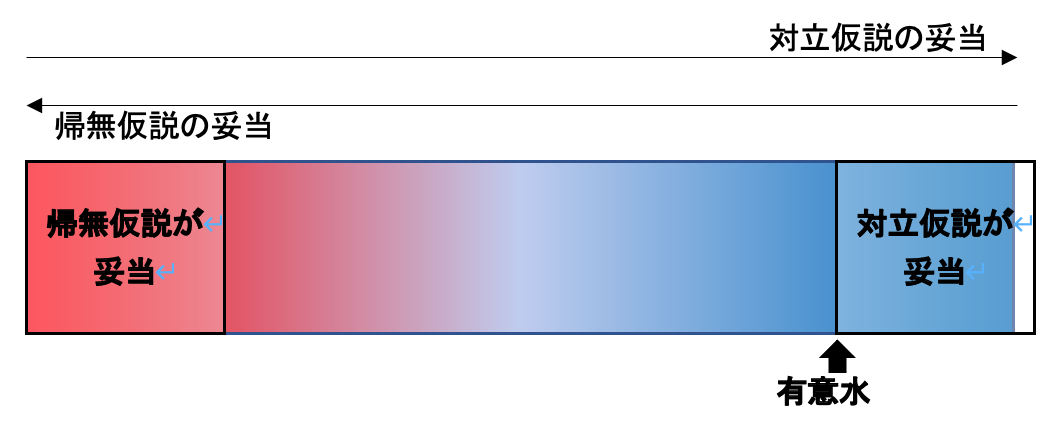
この図を見ると、以下のことがわかると思います。
「対立仮説の妥当性が示された」≠「対立仮説が100%正しい」
統計学では、対立仮説の妥当性が高いときに、「対立仮説が採択された」「対立仮説の妥当性が示された」などと表現されることがあります。しかし、上図からわかるように、あくまでも「仮説が正しい可能性が高い」ということを言っているにすぎず、「仮説が正しい」ことが厳密に証明されたわけではありません。
統計学で、「仮説が100%正しい」ことを証明することはできません。誤解を避けるために、「対立仮説が採択された」とは表現されず、「帰無仮説が棄却された」と間接的に表現されることが多いです。ただ、このような誤解を避ける表現が、かえって統計学を難しく感じさせている原因のようにも思われます。
「対立仮説の妥当性が示されなかった」≠「対立仮説が間違っていた」
「対立仮説の妥当性が示されなかった」≠「帰無仮説の妥当性が示された」
統計学では、どちらの仮説が妥当なのか、結論を出せないことが多いのも特徴の一つです。上図からわかるように、有意水準を厳しく設定すればするほど(図の右側に設定すればするほど)、帰無仮説よりも対立仮説のほうが正しい可能性が高いにもかかわらず、有意水準を満たせず、「対立仮説の妥当性が示されなかった」という判断になることもあります。よって、「対立仮説の妥当性が示されなかった」ということは、決して、「対立仮説が間違っていた」というわけでも、「帰無仮説の妥当性が示された」というわけでも、さらには、「帰無仮説のほうが対立仮説よりも妥当」というわけでもありません。
「対立仮説の妥当性が示されなかった」場合に、「帰無仮説が棄却されなかった」と、ややわかりにくい表現がされるのは、このことが理由です。「帰無仮説が採択された」という表現は、「帰無仮説のほうが対立仮説よりも妥当」であるかのような誤解を招くため、適切ではありません。
「対立仮説」と「帰無仮説」は対等ではない
上図から、「対立仮説の妥当性を示すこと」(=「帰無仮説が棄却されること」)は、「帰無仮説が棄却されないこと」よりも、ずっとハードルが高いことがわかります。グラデーションの範囲の中で、有意水準より右側は、全体のわずかな領域にすぎないからです。つまり、仮説検定においては、「帰無仮説が棄却されない」ことのほうが多く、普通のことであり、言わば「デフォルト」です。別の言い方をすると、「帰無仮説」のほうが「有利」なのです。
この点は、統計学の典型的な教科書でもあまり丁寧に説明されていないことが多く、初めて仮説検定を学ぶ人にとって混乱や誤解を招く原因となっています。仮説検定では、帰無仮説と対立仮説の2つがあたかも平等に比較されているかのように誤解する人もいるかと思います。
先ほど「デフォルト」という言葉を使った通り、「帰無仮説」は通常、「○○には効果がないこと」「▽▽は△△と同等であること」「◇◇は◆◆に影響していないこと」のような、発見とは言えない、驚きようがない、ありきたりとも思える内容となることが多いのです。一方で、「対立仮説」は、「○○には効果があること」「▽▽と△△には違いがあること」「◇◇が◆◆に影響していること」のように、驚くべき内容、新発見といえる内容となることが多いのです[2]。
仮説検定では、「対立仮説」は、その仮説が正しい可能性が十分高いときに限り、「妥当である」と判断されます。逆に、得られたデータだけでは、帰無仮説と対立仮説のどちらが妥当か判断できないとき、対立仮説が正しいという可能性が十分高いとは言い切れないときは、「帰無仮説を棄却しない」と判断されます。つまり、驚くべき発見とは言いきれない、という判断を下すわけです。
教科書の仮説検定を理解する準備運動
ここまでで仮説統計の考え方のエッセンスを説明しました。一般的な統計学の教科書では、この一連の流れの中で、t値、z値、正規分布、t分布、χ2分布、自由度、棄却域、採択域、P値、第1種の誤り、第2種の誤り、検出力(検定力)などの様々な用語や概念も一緒に学んでいくため、
「そもそも仮説検定では何をしようとしているのか」
「帰無仮説を棄却するとはどういうことなのか」
といった本質がわかりにくくなってしまっています。本質がわかっていない状態だと、マニュアル通りにz値を求め、マニュアル通りに仮説を棄却する、ということになりがちです。仮説を棄却するとはどういうことなのかを正しく理解できていないと、検定結果を正しく考察することができませんし、検定結果に基づいたアクションも不適切なものになってしまうでしょう。
仮説検定の発展的なケースを考える
一通り、仮説統計の考え方を理解したところで、一段上のステップに進みましょう。
同じコイン投げの例で、次のようなケースを考えます。
主催者「コインには、何もしかけはありません。公平なくじ引きです」
参加者「それなら公平だ」
主催者「Aさんのコインは裏でした。残念。」
参加者A「えー残念」
主催者「Bさんのコインも裏でした。残念。」
参加者B「また裏?残念」
主催者「Cさんのコインも裏でした。残念。」
参加者C「また裏?本当?」
主催者「Dさんのコインも裏でした。残念。」
参加者D「コインおかしくない?」
主催者「Eさんのコインも裏でした。残念。」
参加者E「インチキだ!」
主催者「Fさんのコインも裏でした。残念。」
主催者「Gさんのコインも裏でした。残念。」
主催者「Hさんのコインも裏でした。残念。」
主催者「Iさんのコインも裏でした。残念。」
参加者F~I「・・・」
主催者「Jさんのコインは表でした。おめでとうございます!」
参加者J「え?あ、ありがとうございます・・・」
参加者A~I「・・・10回中、表1回だけだから、やっぱりインチキ?」
ここでも、
- 帰無仮説:コインにしかけはない。表が出る確率は0.5である。
- 対立仮説:コインにしかけがある。表が出る確率は0.5ではない。
とし、有意水準は1%、検定統計量は「コインの裏が出た回数」としましょう。
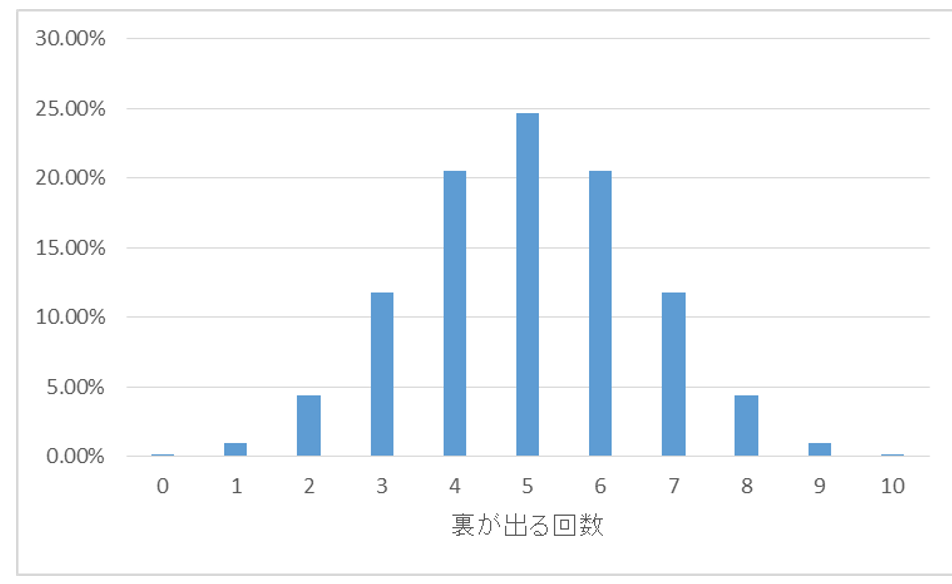
先ほどの計算によると、コインの裏が9回出る確率は、約0.98%ですから、有意水準の1%未満ということで、やはり帰無仮説は棄却されるのでしょうか?
ここからが先ほどの例と異なる点です。
仮説検定では、「帰無仮説が正しければ起こりえない現象かどうか」を判断する際、実際に得られたデータよりも極端な現象の確率を足し合わせて、有意水準と比較します。
コイン投げの例でいうと、実際に得られた現象は「コインの裏が9回出る」という現象ですが、さらに極端に偏った現象「コインの裏が10回出る」現象も、一緒に確率計算に加えます。なぜなら、「コインの裏が9回出る」現象が「起こりえない現象」だとすると、「コインの裏が10回出る」現象は、もっと「起こりえない現象」だからです。
つまり、コインの裏が9回出る確率0.97656250%と、コインの裏が10回出る確率0.09765625%を足し合わせて、コインの裏が9回以上出る確率を求めます。この確率は1.07421875%であり、有意水準の1%を下回らないので、帰無仮説は棄却されません。
ここまでの流れを理解された上で統計学の教科書を読むと、仮説検定の全体の流れのなかで、今どのような目的でどういう計算や判断をしているのか、より生き生きと分かるようになると思います。
統計学の教科書では、コイン投げのような「表」「裏」の2択しかないような単純な確率事象ではなく、正規分布などの複雑な確率事象を扱います。そのため、統計検定量として、「z値」や「t値」のような複雑な数値が登場します。そして、その統計検定量の確率を求めるために、t分布、χ2分布、自由度のような難しい概念が必要となるのです。さらに、正規分布もt分布も、連続的な確率分布であるため、その確率を求める際に「積分」というさらに厄介な概念が出てきてしまいます。
正規分布は、身近な現象によくあてはまる確率分布なので、教科書では「最も基本の仮説検定」として正規分布に従う現象を取り上げるのが一般的なのです。正規分布に従う身近な現象でも仮説検定ができるようになるには、教科書に出てくるような検定まで習得する必要があります。
しかし、初めて統計学を学ぶ方々にとって、いきなり正規分布から入るのはハードルが高く、その前段階として、もっとシンプルな確率事象で、仮説検定の全体像をつかむことが有効なのではないかと思います。
執筆担当:ヤン ジャクリン (データ分析官・講師)
[1] 帰無仮説を「採択する」と表現する人もいますが、「帰無仮説を棄却しない」「帰無仮説は棄却されない」と表現するのが適切です。積極的に帰無仮説の妥当性が示されたわけではないからです。
[2]「驚くべき内容、新発見といえる内容」という表現は、このような例が多いというだけであり、どちらを帰無仮説、どちらを対立仮説にするかの基準ではありません。前述のとおり、帰無仮説は「等号(=)」を使って表せる仮説をあてはめます。「○○には効果がないこと」「▽▽は△△と同等であること」「◇◇は◆◆に影響していないこと」のほうがむしろ驚くべき内容、新発見といえる内容であるケースであったとしても、「等号(=)」を使って表せる仮説を帰無仮説とします。ただし、このような場合の仮説検定は注意が必要です。帰無仮説と対立仮説は対等ではないため、どちらが正しいか結論を出せない場合は、帰無仮説は棄却されません。すなわち、「驚くべき内容が正しい可能性は否定されなかった」という結論になります。この結論自体は正しいのですが、あたかも「驚くべき内容が正しかった」かのように誤解されて独り歩きしてしまう危険性があります。このような状況で正しい判断ができるためには、「第1種の誤り」「第2種の誤り」「検出力(検定力)」といった内容を理解しておく必要があります。