v.学習モデルの性能評価
教師あり学習の際には、学習させたモデルでどの程度正しくラベルが付与されたかを数値化することが可能です。この作業をモデルの性能評価を行うと言います。分析者が最も関心がある事項は、そのモデルは未知のデータに対してどの程度の精度でラベルを付与できるか、という点です。学習させたデータは高精度でラベル付与が可能である一方で、未知のデータに対してはほとんど予測力がない状態にあることを「過学習(Over Fitting)」と言います。学習させたモデルが過学習に陥っていないかを確認する手段として、全データの80-90%程度を学習用に、残りのデータを評価用に分け、評価用データに対して「学習モデルが付与したラベルと正解ラベルが合致するか否か」を検証することが挙げられます。代表的な検証の手法としては、受信操作特性(ROC)曲線があります。
各手法を説明する前に、まずは二値ラベル(陽性および陰性)を例にして正解と不正解の場合分けを考えてみましょう。すべてのパターンは以下の表のいずれかに当てはまります。
| 正解ラベル | |||
| 予測ラベル | 陽性 | 陰性 | |
| 陽性 | $TP$ | $FP$ | |
| 陰性 | $FN$ | $TN$ | |
この表は混同行列(Confusion Matrix)と呼ばれます。$TP$等の記号は、予測ラベルが正解ラベルと一致($T$)または不一致($F$)で、尚かつ、予測ラベルが陽性($P$)または陰性($N$)のデータの個数を表します。つまり、$TP$は予測ラベルが陽性で正解だったデータの個数を表します。
性能評価の際によく使用される指標として、以下のようなものがあります。
| 名称 | 定義 | コメント |
| 正解率(Accuracy) | 予測ラベル全体の正答率を表す | |
| 適合率(Precision) | 陽性と予測したラベルの正答率を表す | |
| 再現率(Recall) | 正解ラベルが陽性の正答率を表す | |
| F値 | 適合率と再現率の調和平均をとったもの |
※調和平均は「率」を表す数値同志の平均値を正しく出すための計算です。
少し理解するのに時間がかかるかもしれない点に、適合率と再現率の違いがあります。例えば、ある疾病の検査薬の効果検証実験を考えてみます。適合率は、検査薬で陽性と判断された患者が実際に病気である確率を表します。一方で再現率は、病気である患者に対して検査薬が正しく陽性を示す確率を表します。「高適合率で低再現率」の検査薬とは、陽性と判断された人は高い確率で病気にかかっていますが、実際は病気である人を陰性と判断する確率も高いということです。ここまでくれば、「低適合率で高再現率」の検査薬とは、大抵の人を陽性と判断する、いい加減な薬のことだと分かると思います。
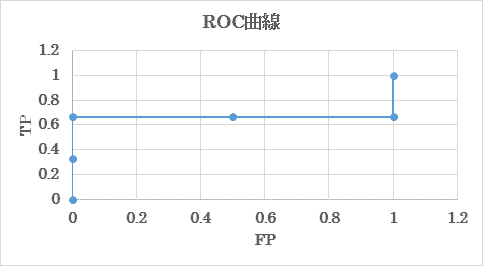
それでは、学習モデルの性能評価に良く用いられるROC曲線に関して説明していきます。ROC曲線では、各々のデータの陽性確率の閾値を変化させたときの「$TP$の割合」と「$FP$の割合」をプロットしていきます。例えば、以下のような表を考えます。
| 陽性確率 | 0.1 | 0.3 | 0.6 | 0.8 | 0.9 |
| 正解ラベル | $T$ | $F$ | $F$ | $T$ | $T$ |
陽性確率の閾値を0.3として、それ以下を陰性($N$)のグループ、それより大きいグループを陽性($P$)と考えたとします。$N$を青、$P$を赤で表を塗りつぶしてみると、以下の表のようになります。
| 陽性確率 | 0.1 | 0.3 | 0.6 | 0.8 | 0.9 |
| 正解ラベル | $T$ | $F$ | $F$ | $T$ | $T$ |
この時の$TP$の割合を考えます。3つの$T$のうち2つが$P$に入るため、$TP$の割合は0.67となります。一方で$FP$の割合は、2つの$F$のうち1つが$P$に入るので、$FP$の割合は0.5となります。以上から、閾値が0.3の時の座標 ($FP, TP$) はそれぞれ (0.50, 0.67) と計算できたので、この点をプロットします。陽性確率の閾値を0.0から1.0まで変化させ、全てのパターンに対してプロットすることでROC曲線が得られます。今回の表を用いると、下のようなグラフになります。
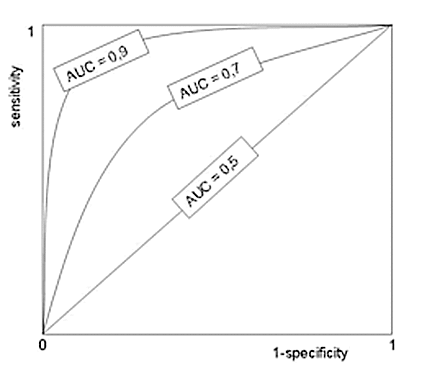
ROC曲線はその性質上、曲線が左上の点 ($FP, TP$) = (0.0, 1.0) に近づくほど、そのモデルの性能が良いことを示します。どれだけ近づいたかを定量的に表す数値として、AUC (Area Under the Curve)があります。AUCは、ROC曲線の下側にできる領域の面積の大きさを表し、0.0~1.0までの値をとります。(下図参照)