現在の機械学習分野を概観するための基礎知識　　～一般的な分析業務の手順とその留意点～ (2)

ii.データ理解と特徴量の抽出

データ入手後には、そのデータの性質を理解し、機械が理解できるようなフォーマットに変換する（特徴量を抽出する）フェーズに入ります。この作業が分析業務の中でも最も重要かつ難易度の高いタスクになります。

データの性質理解には、ビジネスモデルとデータ取得システムに関する深い理解や洞察が必要になるケースがほとんどです。実際の業務で良く問題になり、かつ、分析結果にも影響を多分に与える要素の一つが「欠損値」の取り扱いです。データに欠損が生じる原因として考えられる要因は案件によって異なるため、その対処法も千差万別です。欠損値を補完するか否か、という根本的な部分から考えていく必要があります。また、分析アルゴリズムによってはNull値を許さないものも存在するため、分析に関する知識も必要です。

上述のデータ理解は人間が行うので、どのようなデータ構造でもある程度は進めることができます。しかし、その生データが機械も理解できるような形式になっていることは稀で、また、理解できたとしても情報量の過不足が発生し、分析精度が向上しない要因になります。そこで、特徴量を抽出するという作業が発生します。

機械が理解できる形式とは、基本的にはベクトルまたはテンソル形式になります。ここで言うベクトル（またはテンソル）とは、物理学で用いられるような時空間ベクトルとは異なり、単に配列構造をもった数値データのことを指します。例えば購買履歴データの分析であれば、

[（購入日時），（商品ID），（購入店舗ID），（商品価格）]
のようなデータ構造がそれに該当します。データによっては、このベクトルの次元を何千、何万にも肥大化させ、膨大な情報を機械に教えることも可能です。しかし、情報量を多くしていくことで分析精度も単調に上昇していくかというと、答えはNoです。「次元の呪い」と呼ばれる現象により、予測精度はあるところで頭打ちになり、その後は悪化の一途をたどることが分かっています。

次元の呪いとは、データの高次元化が進むほど、分析の予測精度の向上が妨げられる現象を指します。その主な原因は「球面集中現象」と「必要な学習サンプル数の爆発的な増加」に求められます。

球面集中現象は高次元空間がもつ特有の性質によって引き起こされるもので、3次元で生活する人間の直感や常識とは少し乖離があるかもしれません。この現象は結論から言えば、「高次元球体の体積の大部分は表面に近い薄皮部に集中する」というものです。この問題を考える例として、「オレンジ」と「オレンジの皮」の体積比を考えてみましょう。オレンジは真球であり、以下のスケールであると仮定します。

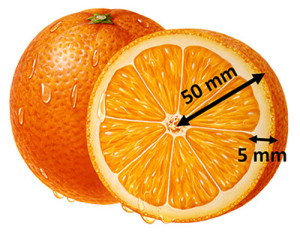
まずは、オレンジ全体の体積$ V_{all}$ を、オレンジ全体の半径$r$を用いて求めてみましょう。

$V_{all} = \frac{4}{3} \cdot \pi \cdot r^3 \approx 524[cm^3] $
次に、オレンジの皮の体積 $V_{skin}$ は全体の体積から「オレンジの実の体積」を差し引いたものなので、皮の厚さ$d$を用いて次のように求められます。

$V_{skin} = \frac{4}{3} \cdot \pi \cdot r^3 – \frac{4}{3} \cdot \pi \cdot (r-d)^3 = \frac{4}{3} \cdot \pi \cdot r^3 \{ {1-(1-\frac{d}{r})^3} \} \approx 142[cm^3] $
したがって、オレンジ全体の体積に対する皮の体積の割合$\delta V$は、

$\delta V = \frac{V_{skin}}{V_{all}} =1-(1-\frac{d}{r})^3=0.271$
となります。全体の体積の1/4程度がオレンジの皮で占有されている計算です。

それでは、$n$次元のオレンジの体積比はどうなるでしょうか？一般に、半径$r$の$n$次元の球の体積$V$は次のように表すことができます。

$V_{all} = c_{n} \cdot r^n$
ここで、$c_{n}$はその次元に対応する係数を表し、3次元の場合は$4\pi/3$に一致します。同様に、皮部分の体積は、

$V_{skin} = c_{n} \cdot (r-d)^n$
となるので、$n$次元のオレンジ全体と皮の体積比は次のように表されます。

$\delta V = 1-(1-\frac{d}{r})^n$
横軸に次元数、縦軸に体積比をとってプロットしたのが次の図です。

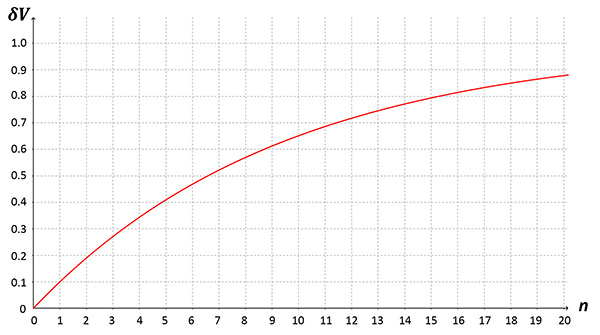
3次元では27%程度だった皮の割合が、10次元では約65%、20次元では約90%が皮の体積で占有されていることが分かります。すなわち、高次元球体上にランダムに点をプロットしたとしても、中心部の近傍には点がほとんど存在せず、大部分は表面に付着することを意味します。表面上に集中するということは、中心から見てほとんどの点は等距離にあることとなります。証明は省略しますが、これは各点間の距離分布が徐々に同程度になることと同義となります。したがって、特徴をより正確に反映させようと次元を増やした結果、かえって特徴が消失していってしまうことになります。

次元の呪いを生じさせる要因としてもう一つ、「必要な学習サンプル数の爆発的な増加」もあります。まずは単純な例として、コインとサイコロを1000回ずつ投げる試行で考えてみましょう。両者とも、データの次元としては1次元ですが、その1次元を分割するグリッド数が異なります。コイントスの試行は1次元を2分割（表と裏）し、サイコロを振る試行では6分割（1から6の目）します。なお、この試行を現実の世界で実現するのは非常に骨が折れるので、今回はプログラミングの力を借りて、仮想世界で実験を行いました。その結果の図がこちらです。

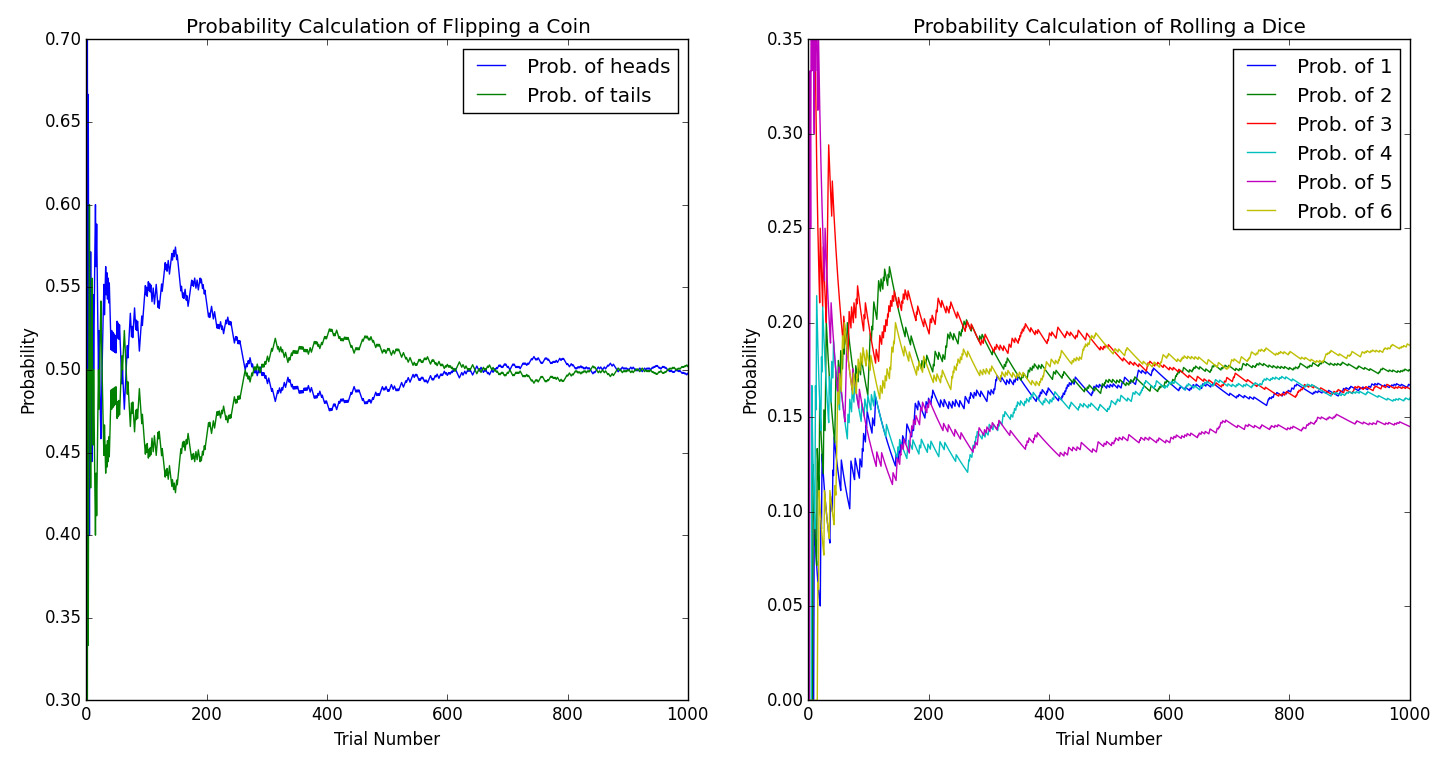
左側のグラフはコイントスを1000回行ったときに、表（head）と裏（tail）が出現する確率が0.5 ( =1/2 ) 近傍に収束する様子を、右側のグラフはサイコロを振ったときの1から6までの目が出る確率がそれぞれ0.167 ( = 1/6 ) 近傍に収束する様子を表しています。両方のグラフにおいて、縦軸が確率、横軸は試行回数を表しているのは共通です。どちらのグラフでも、試行回数が少ないところでは、それぞれの確率がバタついているようですが、回数を重ねるごとに、徐々にそれぞれの真の値に近づいていることが分かると思います。この結果をもう少し定量的に評価してみましょう。
それぞれの事象が起こる確率の算術平均値と標準偏差を次の表にまとめました。

事象	確率の算術平均値 $E(X)$	標準偏差 $\sigma$
表	0.507	0.027
裏	0.493	0.027
1の目	0.156	0.023
2の目	0.176	0.021
3の目	0.189	0.053
4の目	0.156	0.017
5の目	0.148	0.032
6の目	0.175	0.027

算術平均値はいわゆる平均値ですので、なじみ深いものと思います。算術平均値は次の式で求めることができます。

$E(X) = \frac{1}{n} \sum_{i=1}^n X_i$
ここで、$i$は試行回、$X_i$は各試行回における確率、$n$は全試行回数を表します。一方で、標準偏差とは、その平均値がどれだけ揺らぐ可能性があるかを示す指標で、次の式で求めることができます。

$\sigma = \sqrt{ \frac{1}{n} \sum_{i=1}^n (X_i-E(X))^2}$
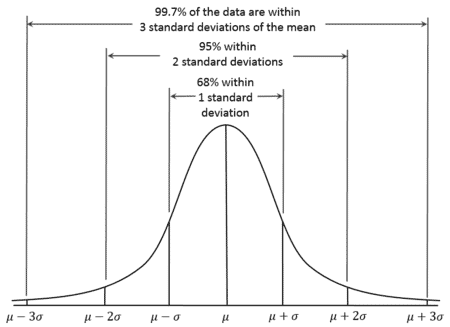
例えば上の表のコイントスで「表」が出る真の確率は、0.507±0.027の範囲の中の値である確率がおよそ68%となります。この68%という数字は統計学の「中心極限定理」をベースにして算出されるもので、この範囲のことを1$\sigma$範囲とも呼ばれます。同様に2$\sigma$範囲、つまり0.507±0.054の範囲の中には約95%の確率で入ってくることも同定理から導かれます。平均値$\mu$、標準偏差$\sigma$のときに、真値が各$\sigma$範囲に収まる確率とその確率分布（ガウス分布や正規分布と呼ばれます）を表す概要図を下に載せておきます。（画像出典: 『68–95–99.7 rule』, Wikipedia）

話しを今回の実験に戻しましょう。コインとサイコロを用いたそれぞれの実験において、各事象が出現する確率の平均と標準偏差を見てみると、どの平均値も真値に近く、1$\sigma$範囲の中に真値が含まれていることが分かります。これは、グリッド数に対してデータ数が十分にあるため、統計学がその威力を十分発揮していることの証明でもあります。それでは、試行回数を10回にしてみるとどうなるでしょうか。その結果は、今回は以下の表のようになりました。

事象	確率の算術平均値 $E(X)$	標準偏差 $\sigma$
表	0.259	0.181
裏	0.741	0.181
1の目	0.0	0.0
2の目	0.065	0.042
3の目	0.120	0.067
4の目	0.568	0.087
5の目	0.227	0.161
6の目	0.259	0.123

例えば、この表のサイコロの1の目が出る確率の平均値と標準偏差がともに0になっています。これは、10回の試行の中で1の目が一度も出なかったため、その確率は常に0で、値に変化がなかったことが原因です。値に変化が無かったので、値の揺らぎの指標である標準偏差も0になってしまった訳です。この統計を信じるとすると、1の目が出る確率は完全に0となりますが、そんなことは実際には有りえません。グリッド数に比べて、データ数が十分大きいという条件をクリアしなければ、信用できない統計値が得られるだけになってしまうということです。
これまではデータが1次元の時のことを考えてきましたが、これを多次元に拡張することを考えていきましょう。多次元化した際に劇的に変化するのはグリッドの数です。下の図は、1次元（$D=1$）から3次元（$D=3$）の空間において、各軸を3つのグリッドに分割したときの様子を示しています。

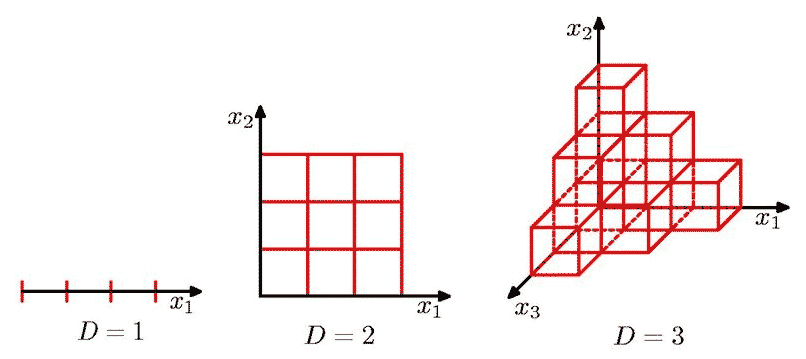
1次元ではグリッド数は3ですが、2次元では9、3次元では27と指数関数的に増加していくことが分かると思います。これらのグリッドの中に入るデータ数が十分になければ、1次元の結果で明らかになったように、信頼できない統計値しか得られません。例えば、1つの軸の分割グリッド数が3であっても、100次元ともなると全グリッド数は$5.1\times 10^{47}$個に跳ね上がります。現時点での全世界のデジタル情報量は40ゼタバイト（=$4.0\times 10^{22}$ byte）と言われていますが、1byteで1つの情報を表せたとしても、それでも遠く及びません。

以上のことから、高次元特徴ベクトルは(1)各データ点の特徴が失われる危険性があり、(2)統計的に有意な値を得るためには膨大な量のサンプル数が必要である、ということが分かっています。これを回避するためには、主成分分析や特異値分解のような高次元ベクトル（またはテンソル）を低次元へ変換するような数学技法が効果的です。特にテキストデータを扱う場合には、基礎的な特徴量（例えばBag-of-Words）は次元数が出現単語数に相当するため、どうしても高次元になりがちです。特異値分解の手法である、潜在意味解析（LSI）や潜在ディリクレ解析（LDA）のような、いわゆるトピックモデルを用いることで高精度分析が可能になることが知られています。分析する手法にもよりますが、トライしてみる価値はあるかと思います。

【参考文献】
『パターン認識と機械学習』