先日M氏がO御大に質問していたのを聞いて、自分も気になったのでまとめてみました。
そもそも勾配ブースティングで目的関数はどのように使われる?
分類問題の話に入る前に、回帰問題を例にして勾配ブースティングの原理を簡単に解説します。
冒頭のM氏の質問ではXGBoostでしたが、ここ数年Kaggleなどでよく使われるLightGBMも含め、基本的なアルゴリズムは全部同じです。
勾配ブースティングの仕組み
$N$個のデータ $[\backslash boldsymbol?]x=x_1,x_2…x_N$と正解データ $[\backslash boldsymbol?]y=y_1,y_2…y_N$が与えられているものとします。
今、勾配ブースティングモデルを$F_T(x,\Theta)$と表すことにします。
簡単に言うと、勾配ブースティングは、決定木を縦に足し合わせたモデルで、各木を$f_i(x,\theta_i)$として、以下のようにあらわすことができます。
$$F_t(x,\Theta_t)=\sum_{i=1}^{T}f_i(x,\theta_i)$$
ここで、$T$は縦につなげた木の数(scikit-learnのGradientBoostingでいうn _ estimators)を意味します。
$\Theta=\theta_1,\theta_2…\theta_T$は各木のパラメータ(木構造、分割の際に用いる特徴量や閾値など)です。
学習プロセス
では、$T$本の木をどう構築していくかですが、一言でいうと予測誤差にフィットさせた木を接ぎ足していきます。
例えば、$t$本目までの木ができていたとして、その時点での暫定モデルを$F_t(x,\Theta_t)=\sum_{i=1}^{t}f_i(x,\theta_i)$と表すことにします。
この時のモデルと正解値との予測誤差$y_i-F_T(x_i.\Theta_t)$にフィットさせて学習したものを、$t+1$番目の木とします。
このようにすることで、新しい暫定モデル$F_{t+1}(x,\Theta_{t+1})=\sum_{i=1}^{t}f_i(x,\theta_i)$は、$t$本目までのモデル$F_t(x,\Theta_t)$で間違ったデータを重点的に学習していく形になります。
損失関数を用いた解釈(勾配降下法)
前項では予測誤差$y_i-F_T(x_i,\Theta_t)$を新たな目的変数として新しい木を作っていきましたが、これを、損失関数と勾配降下法という視点でとらえ直してみます。
まず、以下のように損失関数を定義します。$$L([\backslash boldsymbol?]y,{F_t(x_i,\Theta_t)_{i=1}^N})=\frac{1}{2}\sum_{i=1}^N(y_i-F_t(x_i,\Theta_t))^2$$
これは単純に誤差の2乗和ですが,モデルの予測値$\{F_t(x_i,\Theta_t\}_{i=1,2…N}$を変数とした下に凸な関数としても捉えることができます。
さて,ここからがポイントなのですが,予測誤差$g_i=y_i-F_T(x_i,\Theta_t)$は,下記のように損失関数の勾配として捉えることができるのです。
したがって,「予測誤差に対して新たにフィットした木をモデルに追加する」という操作は、実は、勾配に沿った方向にモデル予測値を修正するということに相当するのです。
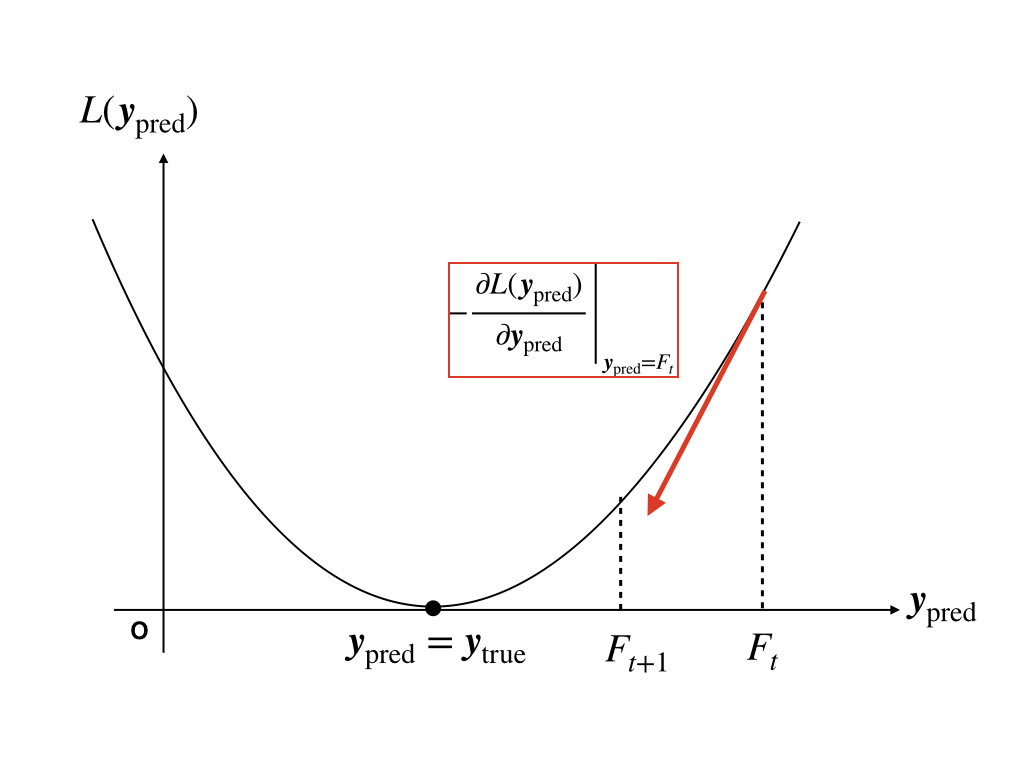
イメージ的にはこんな感じです:
$$F_{t+1}(x_i,\Theta_{t+1})=F_t{x_i,\Theta_t}+f_t(x_i,\Theta_{t+1})\approx F_t(x_i,\Theta_t)-\frac{partial L([\backslash boldsymbol]{y},\{F_t(x_i,\Theta_t)\}_{i=1}^N)}{\partial F_t(x_i,\Theta_t)}$$
この構図,どこかで見たことありませんか…?
そう,勾配降下法になっているのです。
 gradient descent
gradient descent分類問題の場合
回帰問題では二乗誤差和を損失関数として勾配方向に沿って木を成長させていきました。
この方法は、二乗誤差和以外の損失関数でも適用できます。絶対誤差和や,二乗誤差をある閾値から線形に切り替えたHuber損失が使われることもあります。
同じ要領で、分類問題であっても損失関数さえ決めれば回帰の時と同じFormalismに落とし込むことができます。
問題設定
今までと同様,$N$個の説明変数(特徴量)$[\backslash boldsymbol?]x=x_1,x_2,…,x_N$と目的変数$[\backslash boldsymbol?]y=y_1,y_2,…,y_N$が与えられているものとします。
ただし,今回の目的変数は、$K$個のクラスのいずれかとします:$y_i\in1,2,…,K$
対数損失関数の導入
分類問題を扱うにあたり,出力値は各クラスへの分類確率$p_k^{(t)}(x_n),k=1,2,…,K$とします。
この分類確率は、理想的には正解クラス$k=y_n$のみ1をとり,それ以外は0を取るのが望ましいです。
したがってこの時,損失関数$L$は、
- 全データの正解クラスへの分類確率$p_{k=y_n}^{(t)}(x_n)$が1のとき,$L=0$
- 正解クラスへの分類確率$p_{k=y_n}^{(t)}(x_n)$が0に近づくほど$L$は大きくなる
となるように設計するのが望ましいです。
そこで,今回の出発点であった対数損失(逸脱度)を導入します。
まず、各学習データについて、分類確率に対数をとったもの$-\log p_{k=y_n}^{(t)}(x_n)$を損失として定義します。
この値は、$p_{k=y_n}^{(n)}$が1の時に最小値0をとり、確率0に近づくにつれ大きくなることが分かります。
これをN個の全学習データ分足し合わせたものが、下記の対数損失です。
この損失関数を使うことで、分類確率$p_k^{(t)}(x_n)$を直接あてに行く場合と比べ、誤分類時の損失が強調されるので学習しやすくなります。
学習の進め方
前項で定義した対数損失をもとにモデルの学習を進めますが、これには回帰の場合と同様に損失関数の勾配を新たな目的変数として逐次新しい木を構成していきます。
ただし、正解ラベルや確率そのものを当てに行くのは難しいので、いったん回帰モデルを構築してから確率に変換するという方法をとります。
$t$ステップ目までのモデルを$F_t^{(k)}(x)$とします。ここで注意点ですが、多値分類の場合は各クラスごとに異なる木を構築し、別々に学習を行います。
このモデル出力値に、二値分類の場合はlogistic関数を、多値分類の場合はsoft max関数を噛ませることで、確率に変換します。
二値分類
多値分類
これを用いると、対数損失とその勾配は以下のように書けます。
二値分類
損失関数:
勾配:
多値分類
損失関数:
勾配:
$\delta_{jk}$はクロネッカーのデルタといって、$k=j$の時のみ1, それ以外では0をとります。
この勾配を目的変数とし新しい回帰決定木$f_{t+i}^{(k)}(x)$を構築してそれまでのモデル$F_t^{(k)}(x)$に足し合わせることで、新たなモデル$F_{t+1}^{(k)}(x)$を作ります。
ここからまた新たな対数損失の勾配を求め、モデルを更新し、…というステップを繰り返していきます。
まとめ
所々細かいところは端折りましたが、以上が勾配ブースティングのアルゴリズム概要になります。
冒頭の「なぜ対数損失を使うのか?」という問いに戻ると、以下のような回答が挙げられるかと思います。
- 勾配ブースティングでは内部的には回帰決定木を用いて予測を行う
- 分類確率に対数をとった$\log p_k(x)$に着目することで値域が$[0,\infty)$ となり、不正解時の誤差が強調される。
対数をとらずに分類確率をそのまま使って$\frac{1}{2}\sum_{n=1}^{N}(1-p_{y_n}^{(n)})^2$といった量を損失関数として学習を行うこともできなくはないかもしれません。
しかし、$p_k(x)$自身は$[0,1]$区間の値しか取れないので、対数誤差と比べると学習しにくくなるように思います。
ちなみに、対数損失以外に指数損失が使われることもあります。
特に二値分類で指数損失を用いる場合は、AdaBoostという別の手法と一致することが知られています。
参考文献
T.Hastieほか、統計的学習の基礎 ―データマイニング・推論・予測―
通称カステラ本。
標準的な機械学習アルゴリズムが網羅的に書かれた辞書のような本です。
分厚いですが、記述は丁寧なので気になるところをつまみ読みするにはもってこいです。
特に勾配ブースティングを含めたツリー系アルゴリズムが数理的にきちんと書かれた書籍はこれ以外知りません。
scikit-learn
Python機械学習ライブラリの定番です。ドキュメントやGitHubにあがっているコードを読みながら動作を辿ってみると理解が深まります。


















