以前の記事では、ディープラーニングを機械学習の手法の一つとして紹介しました。
従来の機械学習では、高い精度の予測モデルを構築するためには、人がかなりの労力をかけて、データの前加工と特徴量エンジニアリングを行う必要があることを伝えました。それに対して、ディープラーニングでは、精度の高い結果を導くために必要な情報(特徴量)をデータから自ら抽出することができます。このポイントが従来の機械学習手法との主な違いです。
この記事では、ディープラーニングで使われている機器学習アルゴリズムである「ニューラルネットワーク」を説明します。
ニューラルネットワークは、人間の脳神経系を数理モデル化したものです。人間の脳の中の神経細胞(ニューロン)はシナプスを介して接続されています。情報が入ってきた際には、電気信号がある閾値を超過すると化学物質を放出して、このプロセスを通じて、シナプスからシナプスへ情報伝達が実現されます。このようなニューロン間の相互接続と脳の機能をコンピュータで模倣したのがニューラルネットワークモデルです。
ニューラルネットワークの基本要素は多層パーセプトロンと呼びます。図1のように、「入力層」「隠れ層(中間層)」「出力層」の3種類の層から成り立っています。図では説明のために一層のみ表示していますが、一般的にはたくさんの隠れ層から成り立ちます。
図1から見られるように、ある層の中で、各ノードが前後の層の各ノードと接続されています。この構造は全結合層と呼びます。
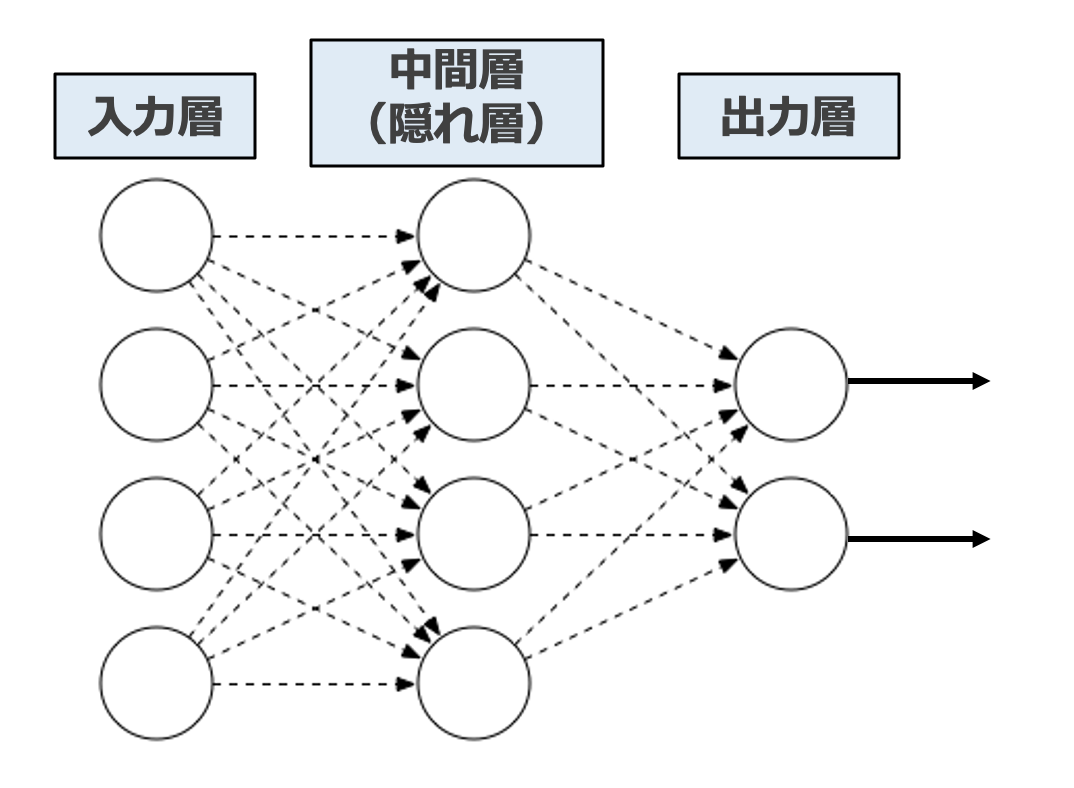
図1: ニューラルネットワークの簡易的概念図
次に図2のように、一つのニューロンに注目しましょう。一つのニューロンでは、信号を受け取り、関数により処理して、次のノードに信号を受け渡すことを行っています。入力と出力の関係性により、隠れ層のニューロン間の結合の強さを「重み」として表しています。ニューラルネットワークにおける「学習」とは、正しい予測を出力できるよう、ニューロン間の結合の強さを層ごとに最適化する作業です。
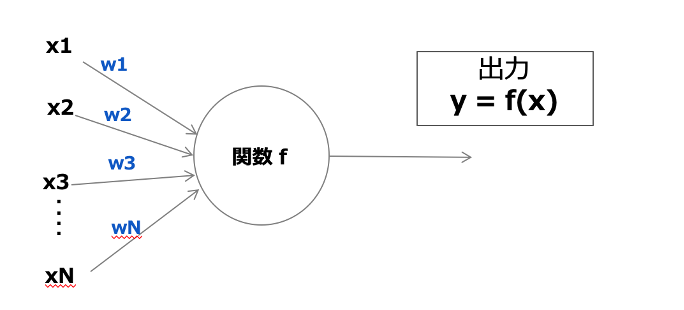
図2: 単独のニューロンにおける信号処理
ニューラルネットワークの学習の仕組みを理解するためには、「重み」と「バイアス」について知ることが必須です。隠れ層は、入力と出力を対応付ける関数に相当します。入力として、前の層からの各ノード入力信号に重み(w)を乗算し、更に定数項としてバイアス (b) を足したものを受け取ります(図3)。
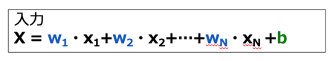
図3: 重みとバイアス
では、次の層にあるノードへどのような結果を出力するのでしょうか?
人間の脳のニューロンも、一つの細胞へ入力された信号はある閾値を超えた際に情報伝達を行います。これと同じように、ニューラルネットワークの中でも、一つのノードに入力されてきた信号を処理して、次に渡す信号を決定づける部分があります。それを担うのは活性化関数です。
図3にあるように、ニューロンへの入力は、(X1 , X2 , …, XN)にそれぞれ重み(W1 , W2 ,…, WN)をかけ合わせた値に、バイアス(b)を足した合計値です。この値を何らかの関数 =活性化関数 に通すことで、次の層に渡す出力が決めます。活性化関数は、非線形関数を使用し、特定の判定基準 (閾値) に従い、情報を処理します。
活性化関数が果たす役割は2つに分類できます(*1)。
1. 計算結果の単位をそろえて比較しやすくする
2. 特徴を際立たせることで比較しやすくする
歴史的には、活性化関数としてシグモイド関数やTahn関数が使用されてきました。一方で、ディープラーニングの実用化の障害となる勾配消失問題が問題視されはじめてから、それを解決してくれる ReLU関数が主流となってきました(図4)。シグモイド関数とTahn関数は「計算結果の単位をそろえて比較しやすくする」役割を果たします。ReLU関数は「特徴を際立たせることで比較しやすくする」役割を果たします。
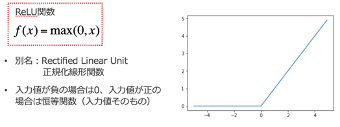
図4: 活性化関数としてのReLU関数
ディープラーニングは基本的には、数多くの隠れ層を持った多層パーセプトロン(ニューラルネットワーク)と解釈して良いです。実用化のために、多層パーセプトロンの弱点である勾配消失問題を解消したり、過学習を低減したりするための工夫が施されています。
例えば画像認識では、「ディープ」なレイヤー構造の中を進めば進むほど、より高度で複雑な特徴を抽出できるようになっていきます。入力側に近い「浅い」隠れ層では、画像の明暗や輪郭など汎用的かつ単純な特徴を、出力側に近い方の隠れ層では、対象物を判別できるような詳細な特徴(例えば目や耳の形)を認識できるように、重みパラメータを最適化していきます。
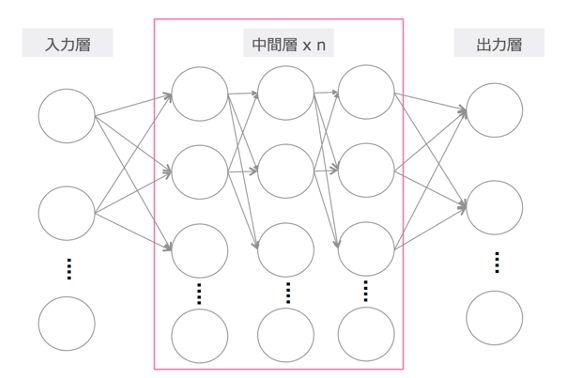
図5: ディープラーニングの簡易的概念図
分析官・講師 ヤン・ジャクリン
















