TL;DR
- 機械学習モデルを構築する際に、関連性が高い特徴量が含まれると色々うまくいかない
- 従来の相関係数だと、数値データのみしか計算できなかったり、非線形な関係は捕捉できないなどの問題点があった
- Predictive Power Score(PPS)は上記の問題を解決してくれる手法なので、特徴量のブラッシュアップの目安としておすすめ
- ただし、PPSは他の特徴量との交互作用を考慮できない点には注意が必要
- Predictive Poser Scoreの詳細はこちら*で確認できます
* Towards Data Science_RIP correlation. Introducing the Predictive Power Score
本題
機械学習モデル構築における特徴量設計が重要なことは言うまでもありません。分析官が知と汗と涙と願いを込めて作成した特徴量。これをどのようにブラッシュアップさせていくかは様々な手法が提案されていますが、今回この記事で紹介するのは、Predictive Power Scoreと呼ばれる特徴選択の手法です。
Predictive Power Score(PPS)は特徴量間の関連性をスコア化する手法です。具体的には、各特徴量のペアを決定木モデルの説明変数と予測変数にとったときの精度をもとにしたスコアを定義算出しています。特徴量間の関連性というと、まず初めに思い浮かぶのは相関分析かと思いますので、相関行列とPPSの違いを明らかにしていくことで、まずはその特徴の概要を説明します。
| 相関行列 | PPS行列 | |
| 計算できるデータ型 | 数値データのみ | カテゴリデータも計算可能 |
| 捕捉できる関連性 | 線形のみ | 非線形も捕捉可能 |
| 行列の対称性 | 対称 | 非対称 |
上記比較表を見れば以下のことがまず分かるかと思います。
- 数値とカテゴリの間の関連性を捕捉できるのが便利
- 非線形な関係性を捕捉できるのが便利
- 相関の場合はX->YとY->Xの方向依存性はないので片方だけ計算すればOKだが、PPSの場合は方向依存があるので両方向ともに計算する必要がある(PPS行列は非対称というのを言い直しただけ)
これだけではイメージが湧かないと思うので、トイデータセットを利用して実際に計算してみました。
データセット
今回はSIGNATEさんの練習用データセットである、国勢調査からの収入予測データセットを使わせて頂きました。性別や年齢、学歴などのデモグラ属性から年収5万ドルより高いか低いかのクラス分類にチャレンジするためのデータセットになります。
| フォーマット | TSV |
| データ行数 | 16,280 |
| カラム数 | 16 |
16あるカラムの各種説明を以下の表にまとめました。ちなみに、すべてのカラムに明示的な欠損はありませんでした。
| カラム名 | 意味 | データ型 | 平均値/最頻カテゴリ | 特記事項 |
| id | 識別データ | 数値 | (IDのため省略) | |
| age | 年齢 | 数値 | 38.6 | 最年少は17歳、最年長は90歳 |
| workclass | 雇用形態 | カテゴリ | Private(69.3%) | 「?」という暗示的欠損あり |
| fnlwgt | 不明 | 数値 | 189975.3 | final weight の略語? |
| education | 教育レベル | カテゴリ | HS-grad (32.0%) | |
| education-num | 教育年数 | 数値 | 10.1 | |
| marital-status | 配偶者の有無 | カテゴリ | Married-civ-spouse (45.8%) | |
| occupation | 職業 | カテゴリ | Prof-specialty (12.6%) | 「?」という暗示的欠損あり |
| relationship | 家族形態 | カテゴリ | Husband (40.2%) | |
| race | 人種 | カテゴリ | White (85.3%) | |
| sex | 性別 | カテゴリ | Male (66.6%)
Femake (33.4%) |
|
| capital-gain | キャピタルゲイン | 数値 | 1131.1 | 株式投資における売却益 |
| capital-loss | キャピタルロス | 数値 | 88.1 | 株式投資における売却損 |
| hours-per-week | 週当たりの労働時間 | 数値 | 40.4 | |
| native-country | 出身国 | カテゴリ | United-States (89.4%) | 「?」という暗示的欠損あり |
| Y | 年収5万ドル以上か否か | カテゴリ | <=50K (75.5%)
>50K (24.5%) |
この記事ではPythonを使って各種計算をしています。本データの読み込み部分は以下のような感じになります。
import pandas as pd
df = pd.read_csv('/path/to/train.tsv', sep='\t')相関行列
まずは相関行列の計算をしてみると、以下のようなソースコード、結果になります。
import matplotlib.pyplot as plt
import seaborn as sns
fig, ax = plt.subplots(figsize=(10, 8))
sns.heatmap(data=df.corr(),
cmap='viridis',
vmin=-1,
vmax=1,
ax=ax)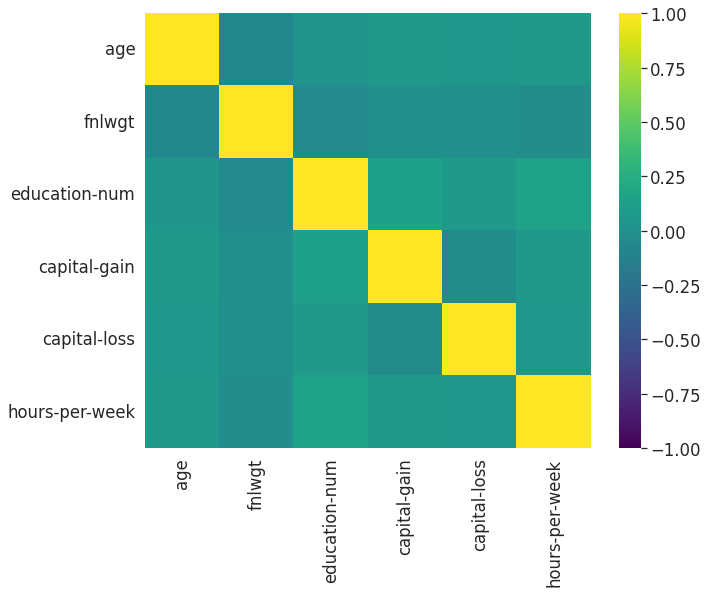
相関行列は数値データのカラムのみしか計算できないので、上記結果の中に肝心の予測ターゲットカラム「Y」が結果が出現せず、分析結果としては全体的に物足りなさを感じます。
PPS
まったく同じデータセットに対してPPSを計算してみましょう。PPSは以下のコマンドで導入することができます。
pip install ppscore
PPS行列の計算は以下のようにたった数行(本質的には1行)で達成できます。
import ppscore as pps
df_pps = pps.matrix(df, random_seed=42)
df_pps_pivot = df_pps.pivot_table(values=['ppscore'],
index=['x'],
columns=['y'])
df_pps_pivot.columns = df_pps_pivot.columns.droplevel()
fig, ax = plt.subplots(figsize=(10, 8))
sns.heatmap(data=df_pps_pivot,
cmap='viridis',
vmin=0,
vmax=1,
ax=ax)
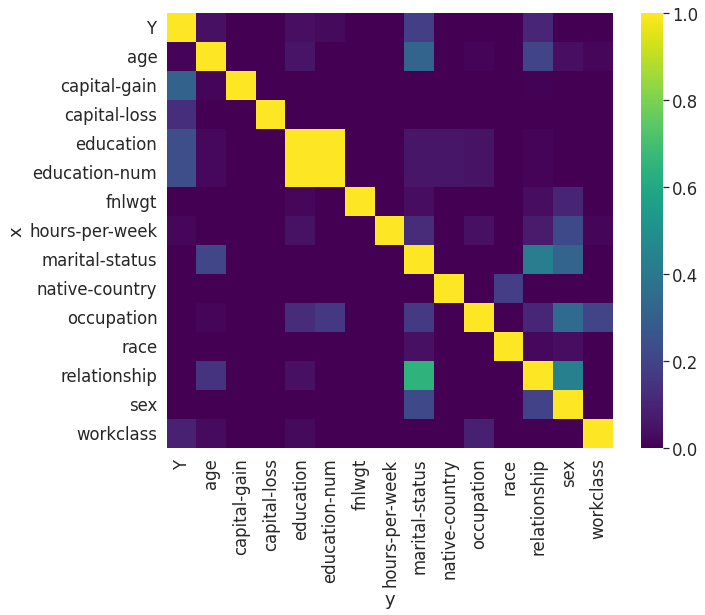
上記を見ると、「Y」も含めたカテゴリ型データの関連性も計算できていることが分かります。結果をもう少し深堀りしてみると、
- education ↔ education-num には双方向の強い関連性がある(PPSは双方向で1.0)
- relationship → marital-status に対してそれなりに強い予測力がある(PPSは0.65)
- 一方で、martial-status → relationship はそこそこの予測力(PPSは0.42)
- 予測ターゲットYに対して最も予測力がありそうなのはcapital-gain(PPSは0.32)
ということが分かります。まずは上記3点に関して集計分析をしてみましょう。
educationとeducation-numの関連性
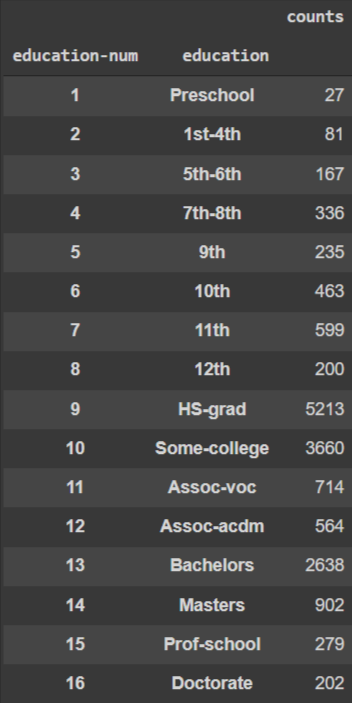
当該2カラムを軸にクロス集計すると下図のようになり、education-numとeducationの間には1対1の関係にあることが分かり、いずれか一つの特徴量のみを残すべきだということが分かります。今回はeducationを特徴量から除外するのが良いかもしれません。なぜなら、教育レベルは名義尺度ではなく順序尺度として扱うべきではないかと推察されるためです。
marital-statusとrelationshipの関連性
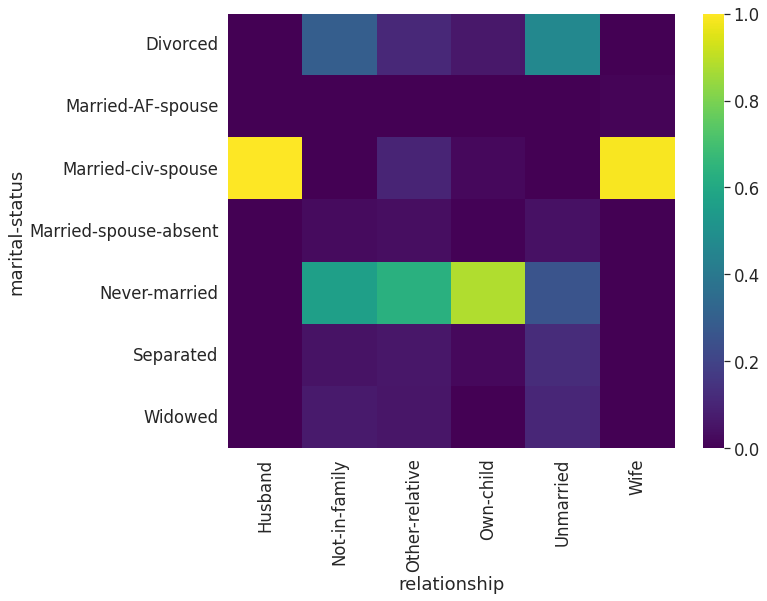
marital-statusとrelaionshipのクロス集計し、relationshipで規格化した結果が上図になります。
- relationshipがHusbandあるいはWifeの場合にはmarital-statushはほぼMarried-civ-spouse
- relationshipがOwn-childの場合にはNever-marriedのケースが多い
などのように、relationshipが決まるとそれに対応するmarital-statusが絞り込めるケースがあることが分かりますが、一方で、
- marital-statusがMarries-civ-spouseでも、relationshipがHusbandかWifeかは絞りこみづらい
- marital-statusがNever-marriedのケースでも複数のrelationsipの選択肢が残る
などのように、marital-status → relationshipは1対Nの度合いが比較的強いことが分かります。これがmarital-statusとrelationshipの間のPPSの非対称性を生んでいる要因と考えられます。したがって、もしいずれか一つの特徴量を残すとするならば、よりPPSが高いrelationshipを選択するのがベターといえます。
機械学習モデルの構築
最後に、Yを予測する機械学習モデルを実際に構築し、PPSスコアとの関係性を確認しました。機械学習モデルの構築にはForecastFlowを利用しました。また、データセットは訓練と検証をそれぞれ7:3に分割し、精度はF1を採用しました。
モデルは以下のようなフローで特徴選択を逐次的に行いました。
- 全特徴量を採用したモデルを構築(これがベースライン)
- educationを除外
- education除外モデルの特徴量重要度およびYに対するPPSが共に低い特徴量をさらに除外
- marial-statusを除外
- モデル4の重要特徴量の最下位workclassを除外
その結果をまとめたのが以下の表になります。
| モデルID | 特徴量数 | 精度 |
| 1 | 14 | 79.4% |
| 2 | 13 | 79.5% |
| 3 | 9 | 80.1% |
| 4 | 8 | 80.1% |
| 5 | 7 | 78.7% |
この結果から、モデル4が特徴選択の最終結果と結論付けられます。特徴量数を5種減らしつつ精度も向上させることができました。また、モデル4の重要特徴量は以下のようになりました。
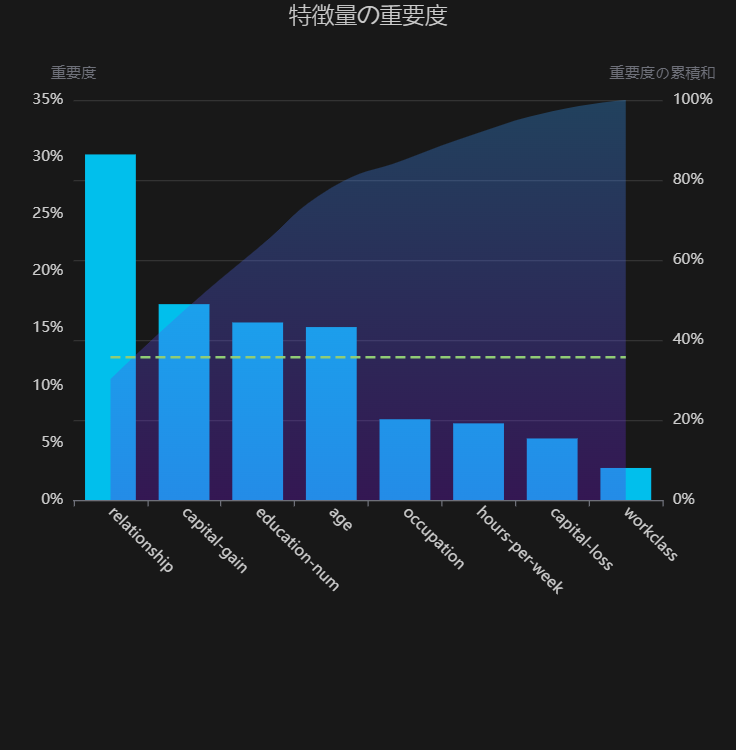
Yに対するPPSで最も高かった capital-gainはモデル重要度の2番目に位置しているので、リーズナブルな結果となりました。一方で、特徴量重要度1位のrelationshipはPPSはほぼ0とかなり低く見積もられていました。これは、ForecastFlowの重要度では他の特徴量との交互作用も考慮しているが、PPSは他の特徴量との交互作用を考慮していないという差異が大きく影響しているのではないかと思われます。したがって、予測ターゲットに対するPPSが低いからと機械的に全部落としてしまうのは危険なことが分かりました。
最後に
PPSを使うことで、データ間の隠れた関連性を簡単に見出すことができました。PPSの計算の仕様上、PPS行列全体を計算するためにはデータの全カラムの2乗個の決定木モデルを構築する必要があるため、カラム数によっては相当計算量が多くなる恐れがありますが、PPSと重要特徴量の2つを見てあげることで、機械学習モデルの軽量化や頑健性の向上につながる特徴選択ができそうな所感を得ることができました。うまく使いこなして皆さんも機械学習モデルの高度化にチャレンジしてみましょう。


















