こちらの記事のAppendixでございます。

「決定木系のアルゴリズムが斜めの分割線を引くのが苦手だ」的なことを申し上げました。
その脚注で「原理的には引ける、程度問題だ」とも。
こう申し上げていたものの、実は「あれ?ほんとに引ける?引けるよな?」と少々混乱していたことはここだけの話でございます。
頭の中で考えていてもよくわからなくなりそうだったので、今回も簡単な実験を通して、決定木系のアルゴリズムがいかにして「斜めの線」を引くのか可視化してみました。
それでは参りましょう。
前回記事のように2次元正規分布に従う乱数を生成しました。ただし今回は簡単のために2グループのみ、さらに分割線がわかりやすいようにグループ間の距離を離しております。
↓こんな感じ。
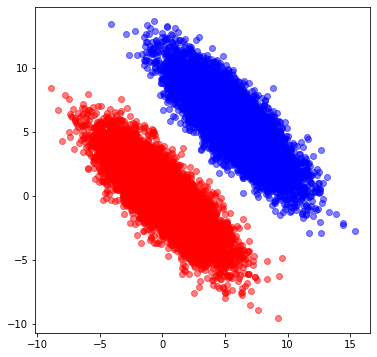
このデータに対して、max_depthを変えつつシンプルな*1決定木分類器にかけ、その時の分割面を確認していきました*2。(max_depthは決定木の深さを表すパラメータです。)
下がその結果です。max_depth=5程度で綺麗に2つのグループを分割できていることが確認できます。逆に言うと、この時分割は全部で31回行われているわけですから、それだけやってようやく斜めの線が表現できている、とも取れるでしょう。
私が「苦手」と言ったのはこのようなイメージを持っていたからでした。
また、「斜めの直線」が引けているわけではないことにも注意が必要です。どういうことかと言いますと、分布の端では分割線がx軸y軸に並行な直線になっていることがわかるかと思います。人間が思うように「斜めにピッと直線を引けば分類できるじゃん」みたいなことはできないのです。
このような時、例えばテスト用データでこの分布がさらに縦長になったとすると、端の方では誤分類が生じてしまうでしょう*3。ちなみに、前回記事のように特徴量同士を足し合わせた新たな特徴量を作成すると、今のデータセットであれば1本の直線で(ほぼ)完璧に分類できます。
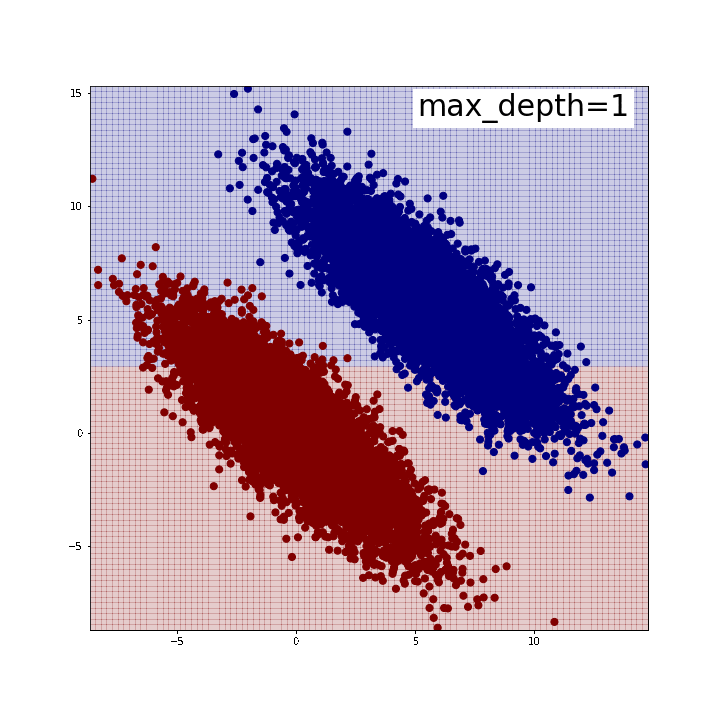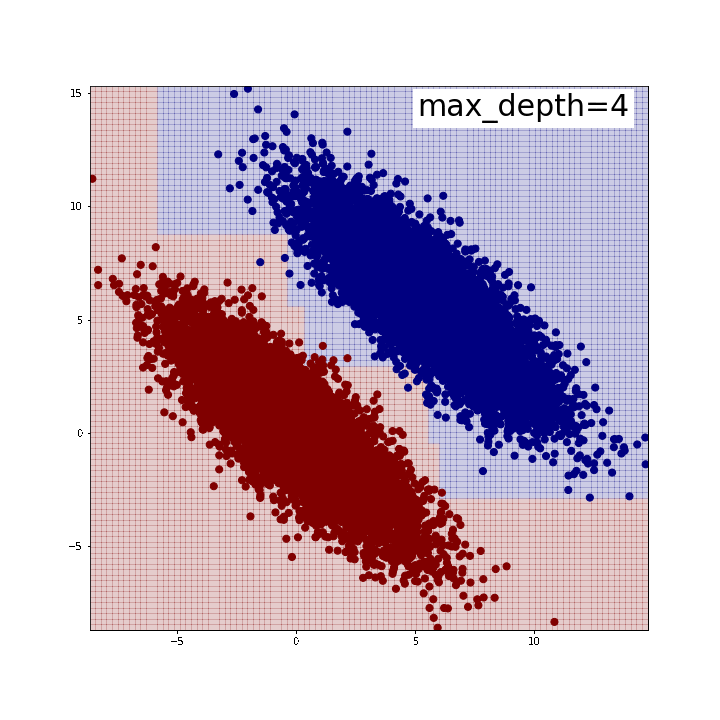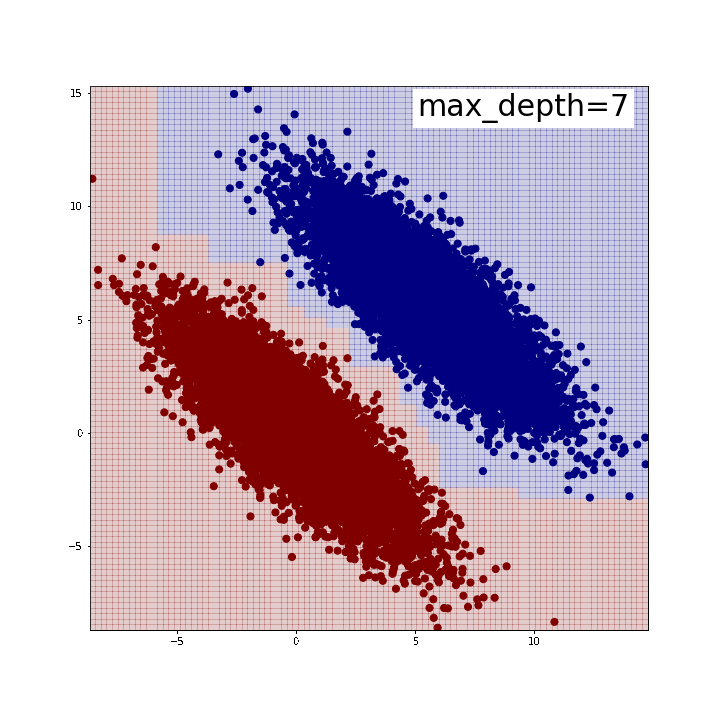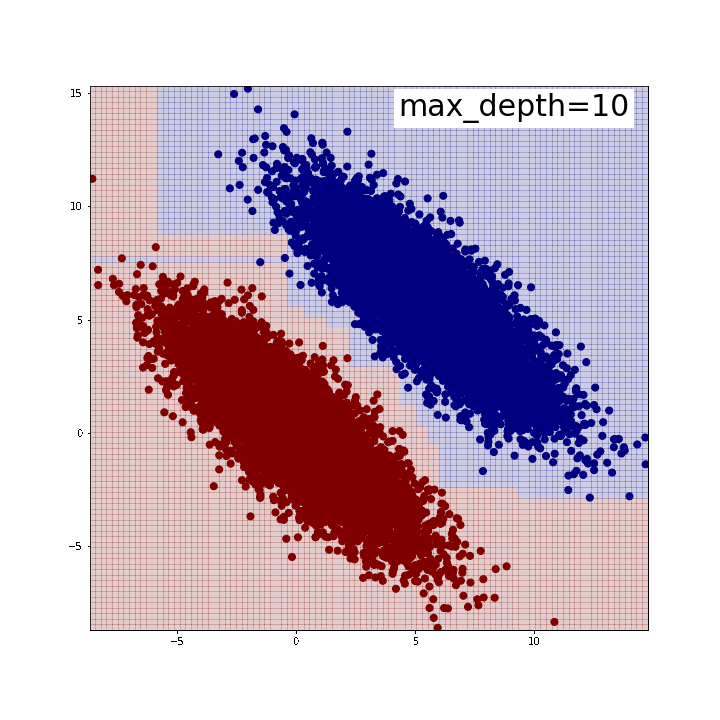
※可視化にはこちらのブログで紹介されている関数を使わせていただきました。
https://qiita.com/yshi12/items/6d30010b353b084b3749
このように2グループのシンプルなケースであれば、いくら苦手とはいえ、常識的なハイパーパラメータ(max_depth)でほぼ完璧に分類できます。しかし、前回記事のように斜めの線を何度も引く必要があるときは、うまく分類できなかったものだと察します。
テストに苦手な問題が出たとき、それが1問であればなんとか解けますが、何問も出てしまっては時間制限内に解けない……そんなイメージではないでしょうか。
博士課程まで理論物理学に従事していた人間とは思えないほど、ざっくりとした説明ですが、こんなものです。常に人間の直感は理論的裏付けに対して先回りします(と思っています)。特に、実務で使うケースにおいては悠長に理論のことを考えている暇がないことが大半でしょう。また、さらに言えば、専門家でない方を説得するのであれば、多少理論がおざなりであっても直感的なわかりやすさの方が重要だったりするものです(と思っています)。
Preferred Networks代表の方も「深層学習は筋のいい実験が大事だ」的なことをおっしゃってました(詳細の記憶が曖昧なのですが、ノリとしてはこんな感じだったと思います)。
私の実験の筋がいいと言うつもりは毛頭ありませんが*4、正確な理論をアレコレ考えるよりも、実験をしてみて感覚を掴む方が時には早かったりすることは確かでしょう。
陸でいくら泳ぎのフォームを練習しても泳げません。海に身を投げましょう。
Appendixにしては長くなってしまいましたが、本記事はこの辺で。
分析官 岡部
*1:バギングもブースティングもしない
*2:train_test_splitのようなことは行っておりませんが、今のように分布がはっきりしているデータではそこまで気にする必要はないでしょう。
*3:「分布が変わってるんだから再訓練が必要でしょ。」もっともでございます。
*4:むしろ「この程度のことを今更……」との誹りを受けそうです。

















