どうも、最近SmartnewsでAIのニュースばかり見ていたら、歌手のAIさんの記事がレコメンドされてきた分析官の岡部です。
この記事では、決定木系アルゴリズムを使用するとき、特徴量同士の四則演算が有用となるケースがあることを、簡単な実験で確認しました。
その結果をまとめていきます。
事の発端
Kagglerに人気のGBDTをはじめとした決定木系のアルゴリズムは非常に強力で、
弊社の製品である自動機械学習ツールForecastFlowでも採用しています。
さて、入社まもないあるとき、そのForecastFlowに突っ込むデータセットを用意していると上司の方から、「この特徴量とこの特徴量の足し算は効きそうだね」と言われ、？？？となりました。
（え？足し算って、、、情報増えてないから、全く意味ないんじゃないの？？？）
などと思ったんですね。
あれから時は経ち、数多のモデルを作っていくうちにだんだんわかってきたんですが、意味は、あります。
とはいえ、身体ではわかってきたものの、やはり頭では納得いかない部分もあるものです。
そこで、今回は簡単な実験を通して、本当に「特徴量同士の足し算」といった特徴量が効果的なのかどうか確認してみました。
結論としては
- 決定木系アルゴリズムでは特徴量の四則演算を明示的に入れた方が良いケースがある
- 自動的に追加すると特徴量の数が爆発してしまうので、ドメイン知識に基づいて追加した方が良い
※対象は機械学習にある程度馴染みがあり、2値分類なども一通り自分でやってみたことがある方、でしょうか。
決定木？？特徴量重要度？？F値？？PDP？？って方は読んでも退屈かもしれません。
実験に使用したForecastFlowに関して
本記事は弊社開発の自動機械学習ツールForecastFlow（内部では決定木系アルゴリズムを使用）を使って実験しております。
このツール、面倒なデータバリデーション、ラベルエンコーディング、ハイパーパラメータチューニング、特徴量重要度・PDP算出まで一気にやってくれるスグレものです。
使い方は以下の動画で解説しておりますのでご覧ください。
今なら無料トライアルもあります（直球）。
決定木系アルゴリズムが苦手なデータ分布
さて、いきなりですが、まずは下図のようなデータを用意します。xとyという2つの特徴量、及び各点に対応する正解ラベルを持つデータです。赤と青の分布それぞれが2つの正解ラベルに対応すると思ってください。
正解ラベルとはモデルによって識別したい対象のことで、例えば
- 解約予測なら「解約・未解約」
- PCR検査なら「感染・非感染」
- ローランドさんなら「俺か、俺以外か。」
みたいなあれです。
このデータ、かなり恣意的ではあるのですが、適当なパラメータの2次元正規分布に従う乱数を、平均を変えて10グループ作成、その後45度回転させたものになります。
（各グループにはそれぞれ10,000点のデータ点が存在）
潰れていて申し訳ないのですが赤のグループは青のグループの下敷きになってます、
想像力を膨らませてご覧ください、、、
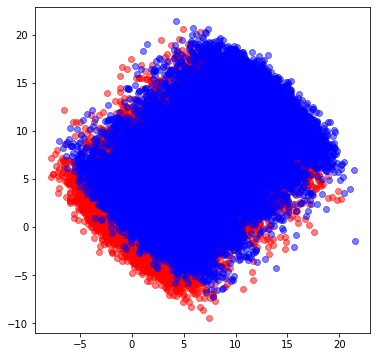
とりあえず、これをForecastFlowに突っ込んで
xとyという2つの特徴量から赤か青かを予測するモデルを作ってみましょう
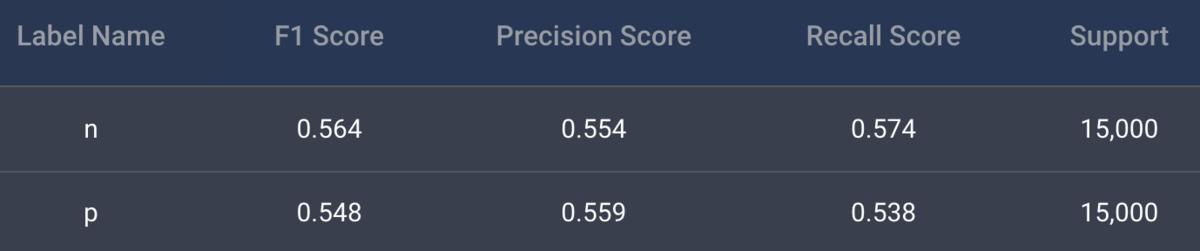
細かい設定などは省きますが、出てきた結果がこちらになります。
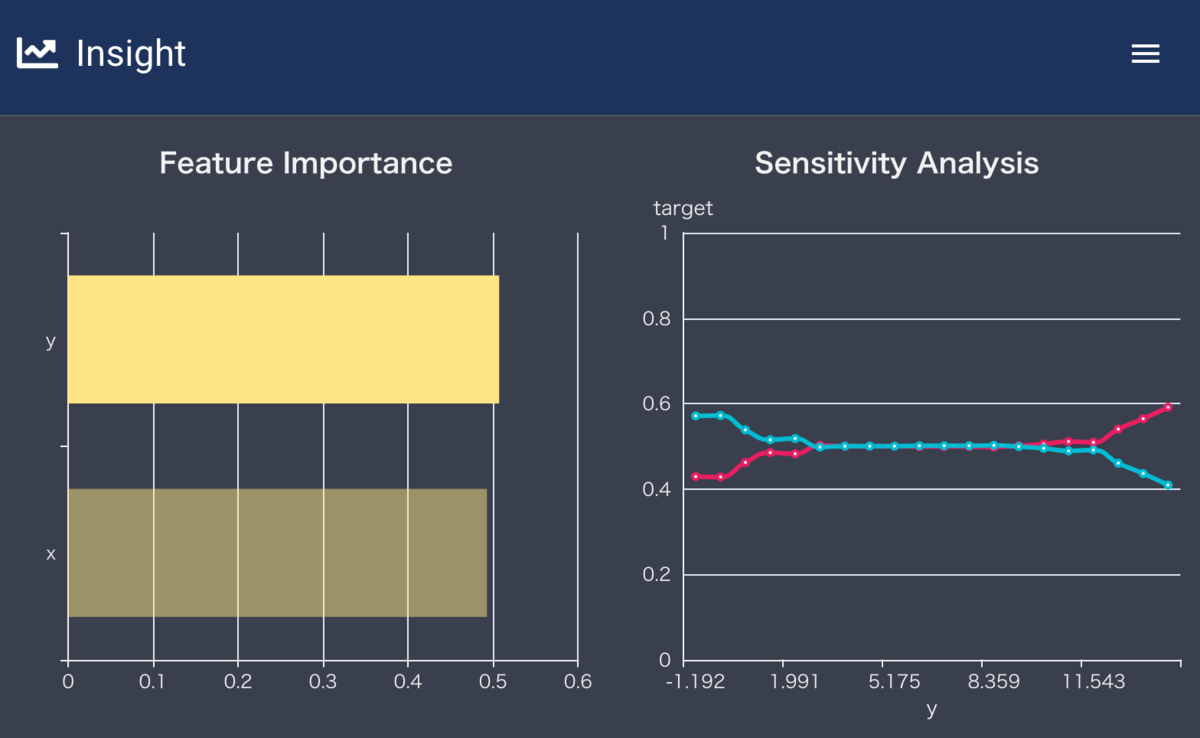yに対するPDP（xに関しても同じような形状）まずは精度を見ると0.55程度と非常に芳しくないものになっています。（細かいことは置いておき、 F1 Scoreを見てください）。
また、Partial Dependece Plot (PDP)を見ると、端の方だけ選択的に分割が行われており、うまくモデルがデータの特徴を捉えきれてないことがわかります。
これは誤解を恐れず言えば、決定木系のアルゴリズムが斜めの分割線を引けないことが原因です*1。
四則演算特徴量を追加した時の結果
では本題。
xとyの四則演算の特徴量(plus, minus, times, divide)を追加して見るとどうでしょうか？
実際に用意したデータをForecastFlowに突っ込み結果をみてみましょう。
なんということでしょう、精度が劇的ビフォーアフターです。
先程の0.55から0.72と大幅に精度が上がっているではありませんか。
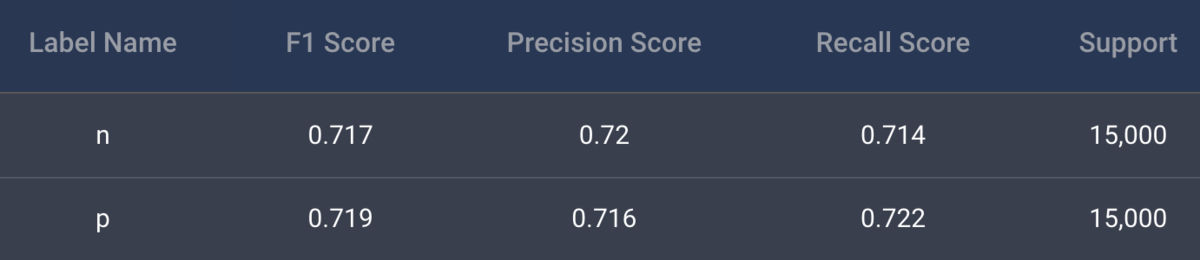
しかしなぜこんなにも精度が向上したのでしょうか？
データの分布及び、PDPを見ると（ある程度）カラクリがわかります。
まずはデータの分布から。
これを見ると1付近, 4付近, ・・・など縦に線を引いてやれば綺麗に分割できそうです。
実際、PDPを見ると対応するところを境にして、赤と青の分割に成功していることがわかります。
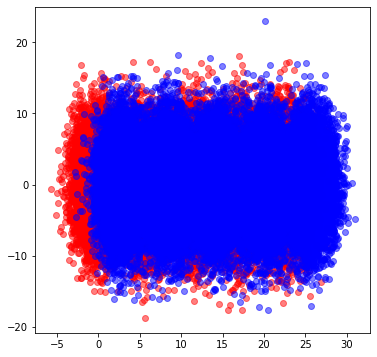
横軸：特徴量plus、縦軸：特徴量minus
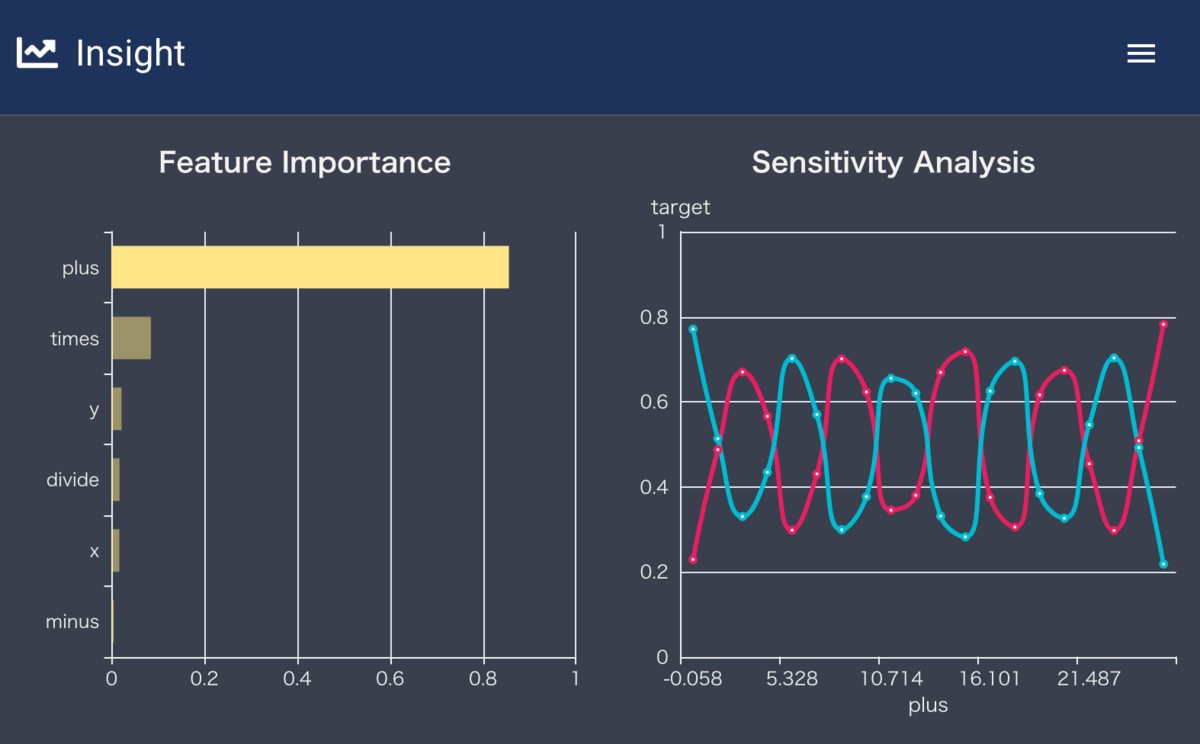
特徴量plusのPDP
以上のように、特徴量同士の四則演算は、時として非常に強力な特徴量を生成できることが確認できました。（今回は足し算が有用となるケースを取り上げましたが、他の演算が有用となるケースもあります）。
理由としては、先ほども少し言ったように決定木系のアルゴリズムが斜めの線を引くのが苦手だからです。
Kaggle界隈には「決定木の気持ちになって考える」という格言がありますが、
今回のケースではまさにその「決定木のお気持ち」を色濃く反映していると言えるでしょう。
決定木先輩は一本気な性格なんです。斜めの線を引くのが苦手なんです。
特徴量同士の足し算という簡単な操作をするだけで、頑固な先輩がズバズバ気持ちよく分割線を引けるようになったわけですね〜
※ここまで読んで、以下のような疑問をお持ちのプロの方、今回は簡単な実験ですのでご容赦ください
- こんな変な分布したデータなんかあるの？ビジネスで言うと例えばどんな時なの？
- ハイパラはどうなってんの？今のデータ分布だと、汎化性能損なわずにもっとゴリゴリにチューニングできるんじゃないの？
あくまでも、こんなケースもあるよ、と言うことをわかりやすく確認するための実験ですので、、、
組み合わせ特徴量の自動生成
じゃあ特徴量同士の四則演算を自動的に追加すればいいんじゃん、楽勝じゃん、と思った方、少しお待ちください。
例えば特徴量が100個あるケースを考えてみましょう。
その時、特徴量の数はいくつになると思いますか？
そうです$4_{100}C_2$で約2万個の特徴量ができてしまうことになります（割り算と引き算の順序性は一旦無視しても）。
500個の特徴量なら50万、1,000個の特徴量なら200万です。
こんなに特徴量があると、流石の決定木先輩も困惑してしまいます。
「この中からいい感じの分割点、見つけといてよ」って言われる決定木の気持ちになりましょう。
あくまでもこうした組み合わせ特徴量は、
- 土曜PVと日曜PVの足し合わせ
- 一購買あたりの平均金額
などドメイン知識を背景とした仮説を元に作って行くのがベターだと思われます。
結論
簡単な実験のつもりが思ったよりも長くなってしまいました。以下結論です。
- 決定木系アルゴリズムでは特徴量の四則演算を明示的に入れた方が良いケースがある
- 自動的に追加すると特徴量の数が爆発してしまうので、ドメイン知識に基づいて追加した方が良い
いずれの場合も、決定木の気持ちになって考えましょう。
実験編と書きましたが、理論編があるかどうかは不明です。
なんとなくイメージはありますが、ちゃんとやろうとするとなかなか骨が折れそうなので、気になる方はぜひ考えてみてください。
*1:厳密に言えば引けます。程度問題です。
