この記事では、データの可視化の手段として、棒グラフや円グラフに比べて、少しだけ珍しい手法を1つ紹介します。平面を領域に分割する「ボロノイ図」と時間経過を動的に表示する「アニメーション」です。
ボロノイ図とは
ボロノイ図とは、平面上に配置された「母点」と呼ばれる複数の座標を基準とし、「どの母点に最も近いか」によって、平面上の座標空間を分割して出来上がる図のことです。
図1に母点の数が 5 個であるボロノイ図の例があります。この図では、赤い点が母点であり、セルのように見える面積が「ボロノイ領域」、これらを区切っているのが「ボロノイ境界」と呼びます。
このような分割を「ボロノイ分割」といいます。
ボロノイ図のポイントおさらい
- 2次元の平面を複数の領域に分割し、それぞれの領域は1つの母点に対応する
- 各領域内の任意の点が対応する母点に他のどの母点よりも近いことが特徴である
- 各セル(ボロノイ領域)は、その中心点(母点)に最も近い点の集合を表す

図1:ボロノイ図の一例
ボロノイ図の作り方
ユークリッド平面の場合、平面上に配置された点同士を線で結び、それによって作成された三角形の各辺の垂直二等分線をつなぎ(これでボロノイ境界ができる)、最後に点同士を結んていた線を消すと、ボロノイ図が作成されます。
※ユークリッド距離以外の距離で平面や最短距離を定義することでボロノイ図を作ることもできます。
また、隣接するボロノイ領域の母点同士を結ぶと、「ドロネー図」と呼ばれる新しい図を描くことができます、ドロネー図はボロノイ図の隣接関係を表す図です。
ボロノイ図の用途
ボロノイ図には多岐にわたる応用が存在する実用性の高い図です。活用のイメージとしては、いくつかの点があるとき、「どの点に一番近い?」を探すことです。ボロノイ図は、「平面上に、いくつかの点が配置されているとき、その平面上の点を、どの点に最も近いかによって分割してできる図」です。
上記のように、ボロノイ図を活用すると、母点からの距離を視覚的に捉えることができます。実際、ボロノイ図は、各母点のボロノイ領域の面積によって、「各母点の勢力範囲」を表すと解釈できます。
以下に代表的な用途例です。
- 店舗の勢力範囲などを可視化し、スーパーの新しい店舗を出店する地域を決める
- 市場調査のための勢力圏やエリア分析に使う
- 散らばったデータを、いくつかの代表データにまとめる(クラスタリングと似ている感覚)
- 最短ルートや最寄の施設を探す時(カーナビなどで活用)
- 災害時における最適な避難場所の割り振りの指標突して使う
アニメーションとは
時間的にデータがどのように変化するのかを表現したい時に、折れ線グラフといった「普通」の時系列プロットを使うことが多いです。これに対して、アニメーションを取り入れることによって、横軸と縦軸を時間以外の情報に使いながら、時間軸というもう1つの次元の情報を付加することができます。
アニメーションを取り入れたグラフは「動くグラフ」です。つまり、時間とともに他の軸で張られた平面上でデータが動きます。
アニメーションは、統計データの時間による変化を「動的に可視化」するのに使われます。特に、人口ピラミッドに適用することが多いのです。他に、気象情報や物理現象の経年情報を可視化するために用いることができます。
図2は、国立社会保障・人口問題研究所のサイトから引用した画像です。日本の人口ピラミッドの推移を表現した「動くグラフ」です(横軸が人口、縦軸が年齢になっています)。ここでは、男女別および、4つの区分(年少・生産年齢・老年(前期・後期))で色分けして人口を表示しています。
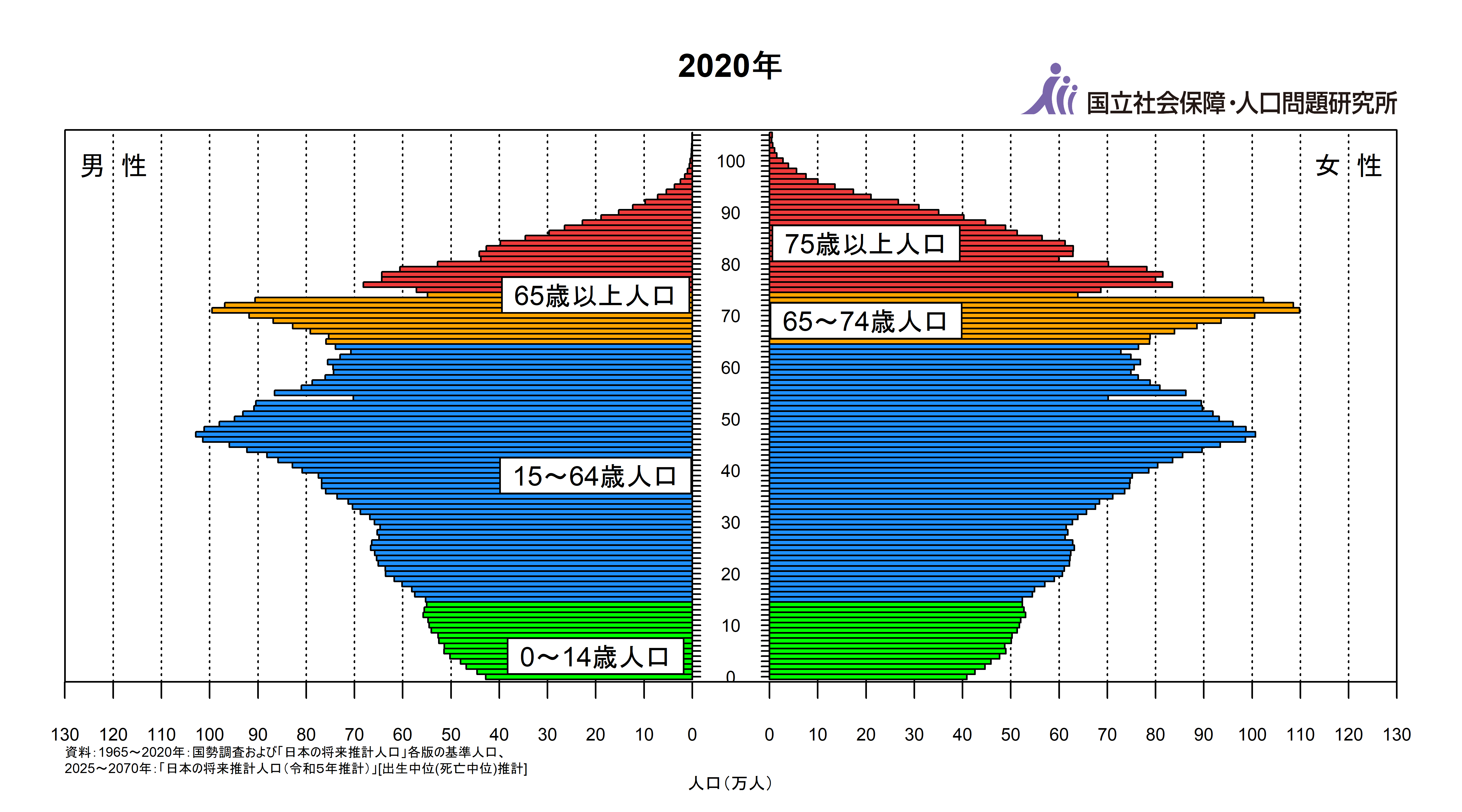
図2
国立社会保障・人口問題研究所のサイトからは、将来の人口を予測したピラミッドも示されています。さらに、人口ピラミッドのデータ(1965~2065年)も公開されています。これらの1つ1つの静止画像を全てつなぎ合わせたものがアニメーションです。
同サイトから取得した動くグラフ(アニメーション)は以下です。このアニメーションより、戦前は一般的なピラミッドの形であったのに対し、高度経済成長期に大きな波が現れます。そして近年は逆三角形の構造になってきていることがわかります。
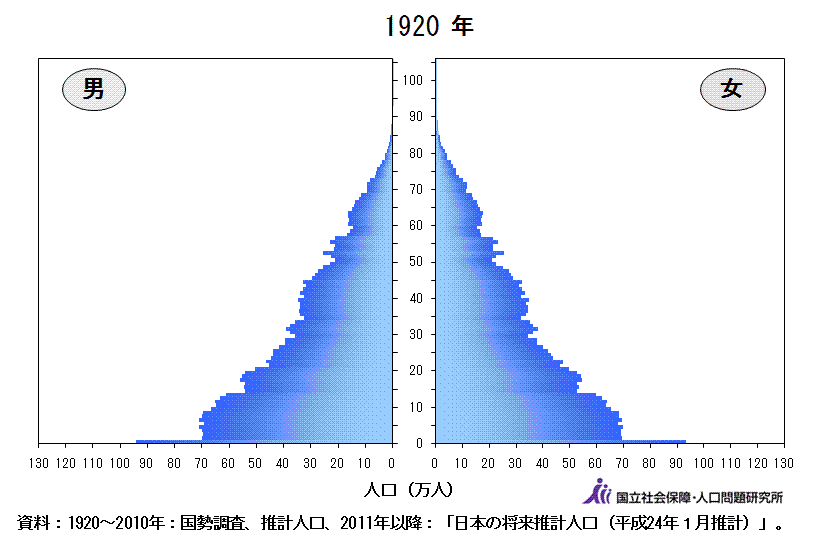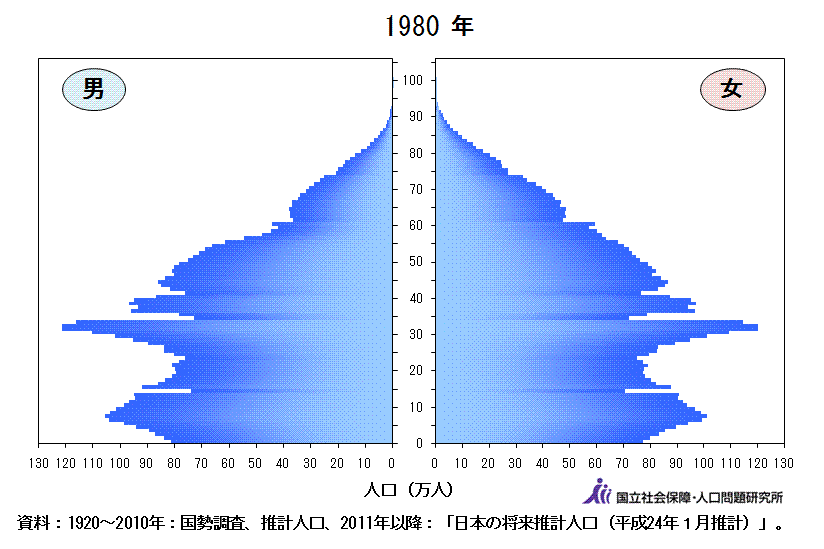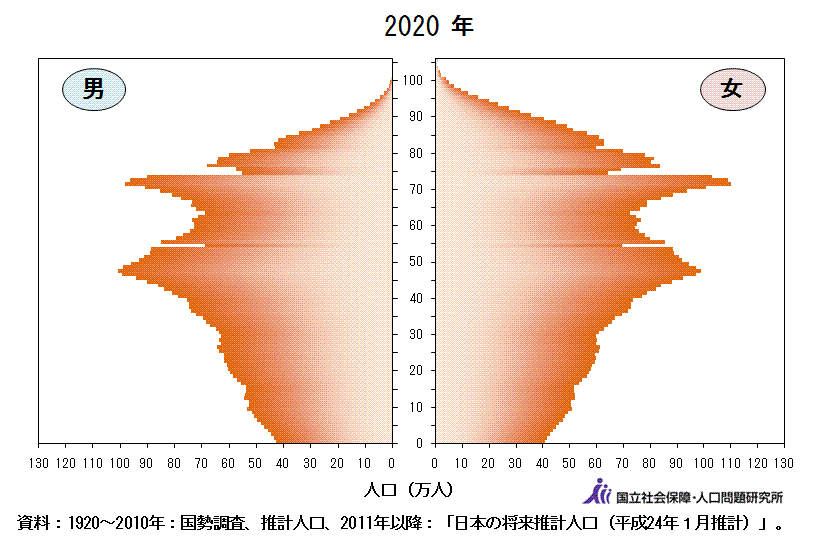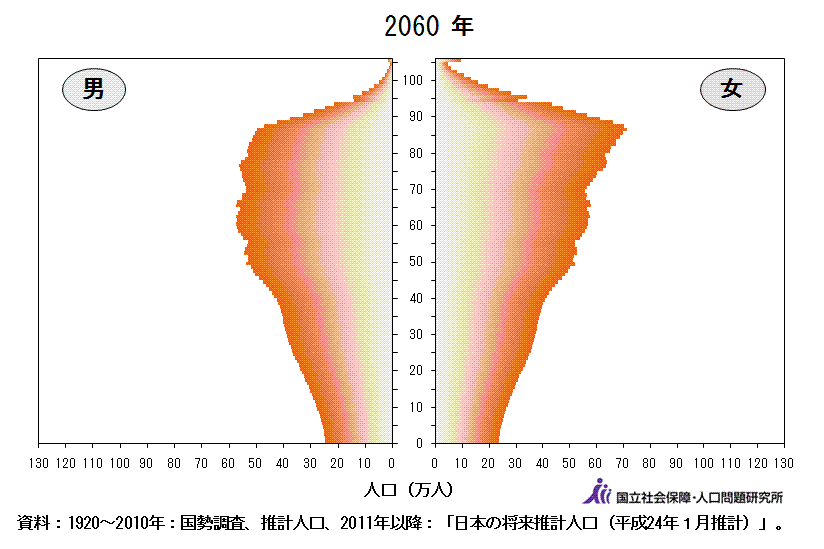
図3
PythonのPlotlyライブラリを用いて、動くアニメーションを簡単に作成することができます。図4に一例を引用します。
例えば、こちらは、世界の各地域について、横軸をGDP/世帯、縦軸を平均寿命とした散布図の年代に従った移り変わりを示したアニメーションです。再生ボタンをクリックすると、1952年から2027年の変化を観察することができます。
時間軸だけではなく、プロット内の丸の大きさで人口のサイズも示しています。こうして複数の可視化の概念を組み合わせて、限られたスペースで効率よく表示しています。


→ 2007年
図4
執筆担当:ヤン ジャクリン (GRI分析官・講師)


















