8.MDS(多次元尺度構成法)
はじめに
多次元で表されるデータを、見て分かり易く、図で表現します。今回はINDSCAL(INdividual Differences SCALing:個人差多次元尺度構成法)モデルを扱います。
古典的方法と現代的方法
本稿では、主座標分析や、Torgersonの方法といった、固有値分解を使うタイプのMDSである「古典的方法」ではなく、先に、仮にでも各対象を位置付ける座標を決めておいてから、漸次布置を改善していく方法を扱います。これを仮に「現代的方法」と称するとき、その中から、2相3元MDSであるINDSCAL(INdividual Differences SCALing:個人差多次元尺度構成法)モデルを実現するものとして、INDSCALプログラムを中心に紹介します。
相(mode)と元(way)
データの形式を指す言葉です。たとえば、相関係数行列は、単相2元データです(図表1.)。クロス集計表は2相2元データです(図表2.)。
図表1.相関係数行列(単相2元データの例)

図表2.クロス集計表(2相2元データの例)
1組の対象を(1種類の対象のセットを)1相(単相)、2組の対象を2相と称します。
相がいくつあるか延べ数を元で表します。相関係数行列(図表1.)は、相は1つですが、元は2つです。同じ相が2つあります。単相2元データ。
クロス集計表は2つの相があります。元の数も2です。だから2相2元データ。
本稿では2相3元データを扱います。2つの相があります。このうち1つの相については、2回出てきます。たとえば、相関係数行列が、日付ごとに4枚(4日にわたって)あるようなケースです。
以下では、単相2元の距離行列が4枚の2相3元データについてみていきます。
INDSCAL(INdividual Differences SCALing)
INDSCALモデルを実現するプログラムでも、ALSCAL(Alternating Least Squares SCALing)プログラムやINDSCALプログラムなど、複数のプログラムがあります。ここでは、主にINDSCALプログラムに沿って話を進めます。
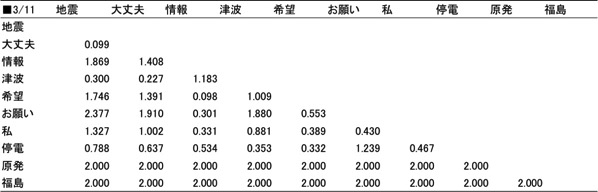
以下の2相3元データを見ていきます。2011年3月11日~14日の4日間にTwitter上でつぶやかれた言葉で、使われた頻度の高かった語の4日間(4枚)の距離行列です。
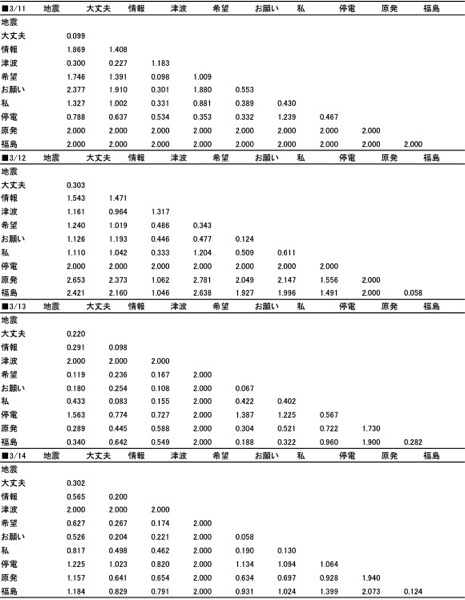
図表3.分析データ(2相3元データ)
各日に固有の布置
まず、何をやろうとしているのか、というところから馴染みがないかもしれません。
図表3.のようなデータ(2相3元データ。単相2元の距離行列が4枚)があります。
これをもとに、とりあえずは語間の位置関係を示す「図」を、日付ごとに1組、4日分で計4組(4枚)求めることを考えます。
先に、結果をみてみます。結果は図で表せられます(この場合は4組(仮に2次元解を採用すれば、1枚×4組=4枚ですし、3次元解を採用すれば最低でも2枚×4組=8枚)の図。4組とは、3/11、3/12、3/13、3/14の4組)。
話がややこしくなるので、ここでは単純に、2次元解を採用して、4枚の図を求めます。
これを図にすると、以下4枚の図になります(図表4.~7.)。なお、先述のとおり、いずれの日付も、2011年、東日本大震災の年の日付です。
図表4.3/11の布置
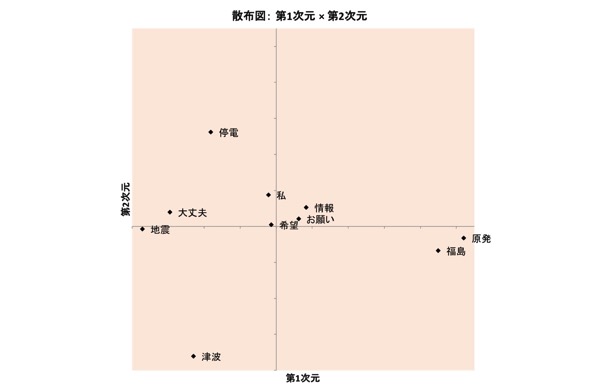
図表5.3/12の布置
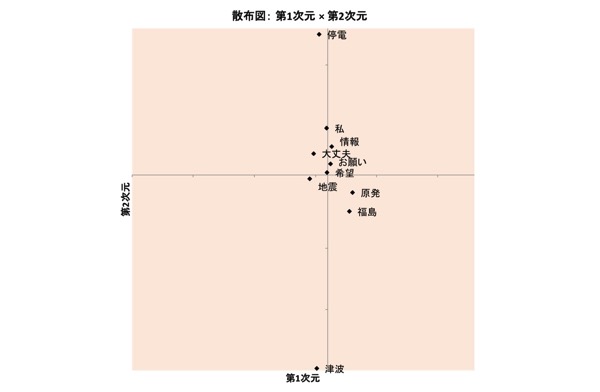
図表6.3/13の布置
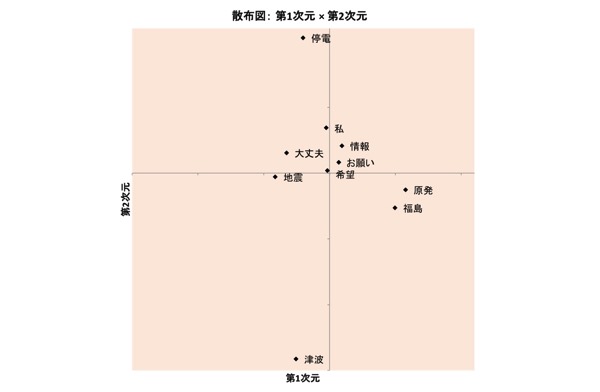
図表7.3/14の布置
これらは、単純に、図上で近いものは近い、図上で遠いものは遠いと、見たままに解釈します。
※たとえばExcelで散布図を描くと、通常、縦軸と横軸の長さは揃いません。ですが、この方法では、出力の距離が極めて重要です。見たままに解釈できるよう、縦軸と横軸は、必ずスケール、長さを揃えましょう。
3/11日の時点(図表4.)では、「地震」と「原発」は離れていました。まだ別の話題だったのでしょう。ところが、3/13日になると(図表6.)、「地震」と「原発」は近づきます。
対象の布置と個人の布置
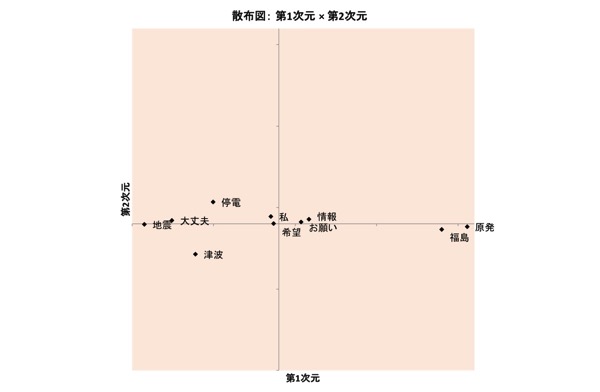
先ほどは4枚の布置が出てきました。もう少し要約できないものでしょうか。そこで、これらの結果を、共通の対象布置と、重み布置という、2枚の図で表すことを考えてみます。
考え方としては、4枚の図を2つの図の掛け算で示す、です。先に「2つの図」を以下に示します。
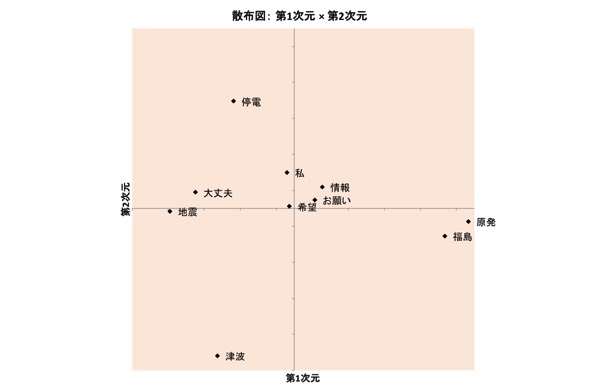
図表8.共有対象布置
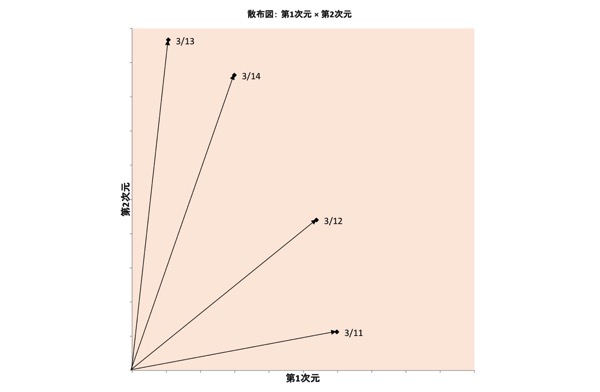
図表9.重み布置
図表8.の、第1次元(横軸)は、マイナス方向に「地震」、プラス方向に「原発」が位置しています。第2次元(縦軸)は、マイナス方向に「津波」、プラス方向に「停電」が位置しています。
図表9.の、たとえば3/13の重みを見ると、第1次元(横軸)は非常に小さい一方、第2次元(縦軸)は非常に大きくなっています。
基本的に重みは、「0」~「1」の間です。図表9.は、縦軸も横軸も、軸の最小値は「0」、最大値は「1」となっています。
図表8.の横軸(第1次元)値に「0」に近い値を、縦軸(第2次元)値に「1」に近い値を乗じた(掛けた)ら、つまり「地震」と「原発」の距離がなくなり(近づき)、「津波」と「停電」が離れた、3/13の布置(図表6.)になります。
今度は図表9.の、3/11の重みを見てみましょう。第1次元は(ほかの日と比べると)大きく(「1」に近く)、第2次元は小さく(「0」に近く)なっています。
図表8.の横軸値に1近い値を、縦軸値に0近い値を、それぞれ乗じたら(掛けたら)、3/11の布置(図表4.)になります。
交互最小二乗法
上記では、専用布置を先に説明し、その後に、それを共通対象布置と重み布置で表現する、という順序で説明しました。ですが計算は、この逆、共通対象布置と重み布置を先に求めます。専用布置は、求まった共通対象布置と重み布置から計算します。
まず、入力データである、非類似度データがあります(図表3.)。必要に応じて、非類似度に加算定数(加算定数は個人ごとに異なる)を加えて距離とします(非類似度が距離であるとは限りません)。
出力データとして、共通対象布置があります(図表8.)。そして共通対象布置が(ランダムであれとりあえず)決まれば、入力データが再現されるように、重み布置(図表9.)を計算できます。そして計算した重み布置を所与として、入力データに近づくように共通対象布置を改善していきます。改善された共通対象布置から、再び、入力データを再現するように重み布置を計算します。この繰り返しです。
この共通対象布置と重み布置を交互に求める手続きは、Stress(布置上の点間距離と非類似度との乖離の二乗が、個々の点間距離と点間距離の平均値との乖離の二乗に対してどれだけあるか)を最小化するまで行います。
こうして互いに(目指す)解との乖離を最小にしていくやり方を、交互最小二乗法と呼びます。
INDSCALプログラムの計算手続
まず、得られているデータから、対象間距離を計算します。必要に応じ、加算定数を計算して加えます(距離行列でない場合、まず距離行列にします)。対象間距離から、内積を計算します。(A)
他方、計算される共通対象布置から、対象間距離を計算します。そして、対象間距離の内積を計算します。(B)
共通対象布置は、その初期値を、ランダムに決めても(ただし,初期布置をランダムに決める場合は、何度か計算してみて、Stressを最小化する解が得られることを確認する必要はあります)、合理的初期布置(とりあえずは古典的方法による布置)を与えても、あるいはすでにある布置を使っても(たとえば4次元解のうち重みの大きい3つの次元の解を、3次元解の初期布置に使う)構いません。なにかしら値を決めれば、計算は始められます。
この共通対象布置から、重み布置を計算します。この際、(A)は確定値です。(B)は求まった共通対象布置から計算されます。最終的に(B)ができるだけ(A)と同じになるように、共通対象布置(と重み布置)を改善していきます。
解釈
まず、適切な次元数を結果から読み取る必要があります。本稿では、説明を簡単にするため、2次元解を採用、つまり、2次元で元データを十分説明できている、ということにしました。ただ、今回のデータについてみると(図表10.)、4次元解くらいまで見てみるほうが良いのかな、とも思われます。
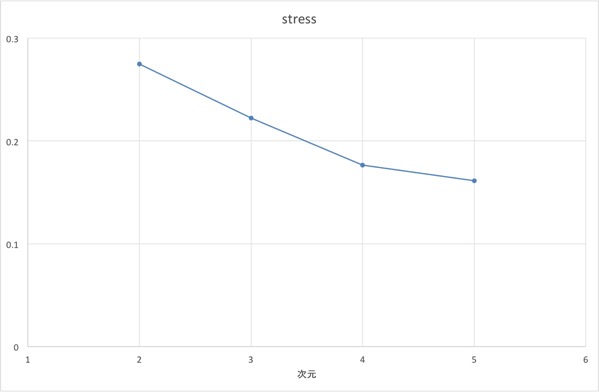
図表10.Stress
なお、この手法は、固有値分解(特異値分解)とは違い、採用すべき次元数が大きいことも多々あり得ることを触れておきます※1。深入りしないでおきますが、固有値分解は、最初の次元から、できるだけ良くデータを説明できるように軸を決めていくのに対し、現代的なMDSでは、先に決めた(指定した)次元数でより良く説明するように軸を決めていきます。
まず、次元の数を決めてから、その次元の解を見ていきます。
次元数が決まったら、その次元数での解を、共通対象布置と重み布置の2つの出力で見ていくことになります(この点は「対象の布置と個人の布置」も参照のこと)。以下には、参考まで、4次元解を採用した場合の布置を示しておきます。
まずは、共通対象布置と重み布置です。
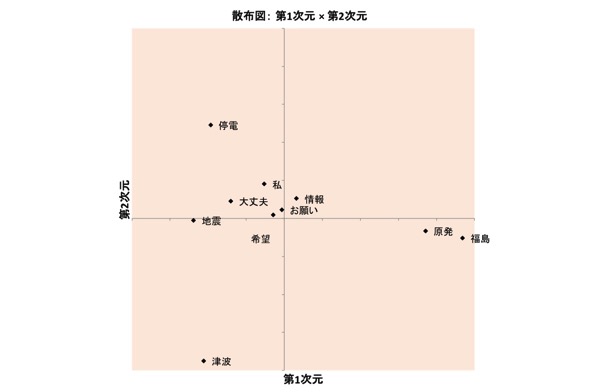
図表11.共通対象布置:1次元×2次元
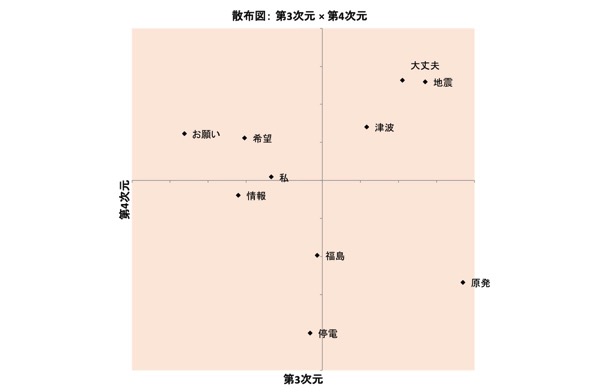
図表12.共通対象布置:3次元×4次元
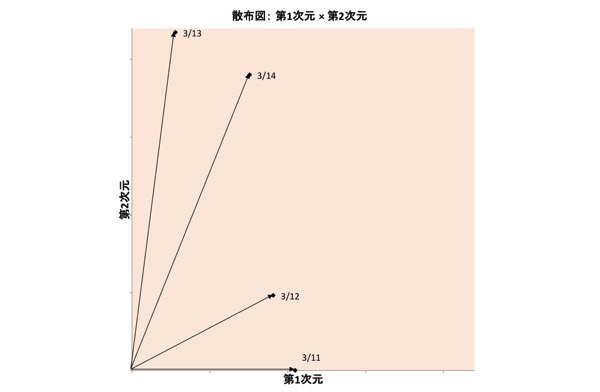
図表13.重み布置:1次元×2次元
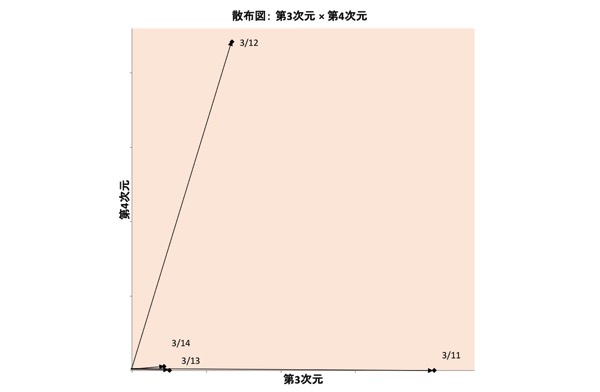
図表14.重み布置:3次元×4次元
3/11~14の各日の布置を求めた場合も載せておきます。共通対象布置と重み布置から、イメージはできたでしょうか。(図表15.~図表22.)
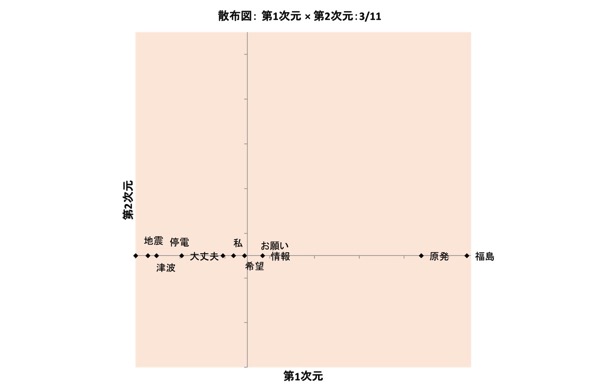
図表15.3/11の布置:1次元×2次元

図表16.3/11の布置:3次元×4次元
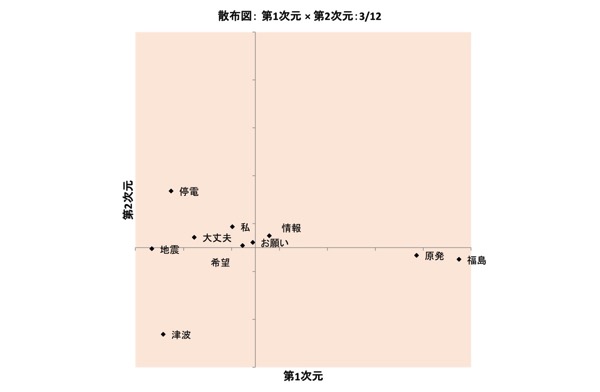
図表17.3/12の布置:1次元×2次元
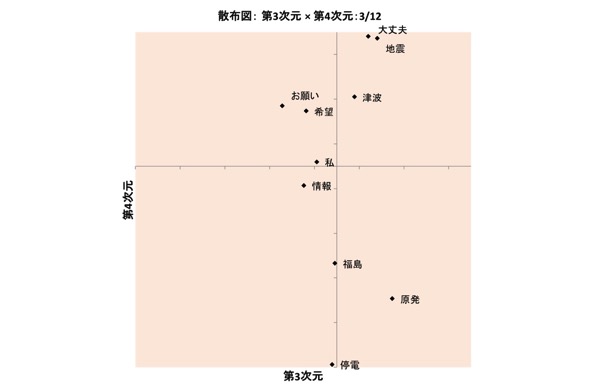
図表18.3/12の布置:3次元×4次元
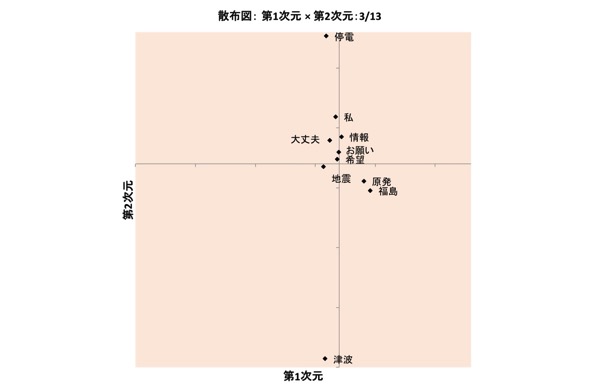
図表19.3/13の布置:1次元×2次元
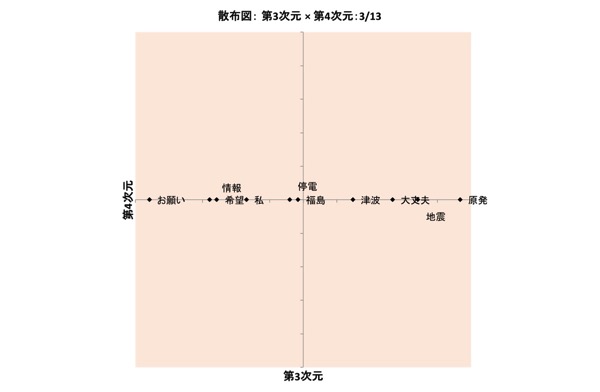
図表20.3/13の布置:3次元×4次元
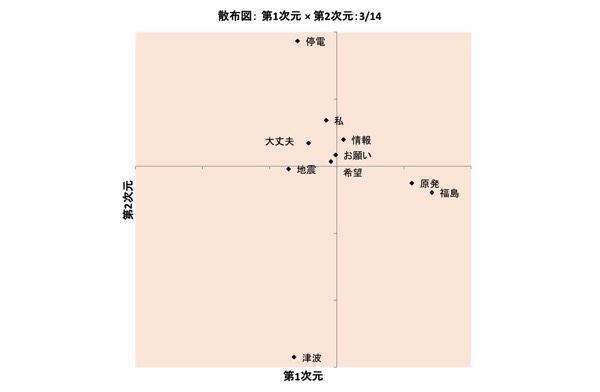
図表21.3/14の布置:1次元×2次元
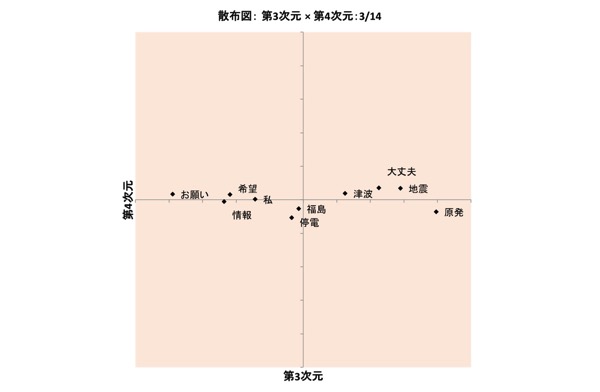
図表22.3/14の布置:3次元×4次元
なお、図表15.、図表16.、図表20.、図表22.では、2つの軸(横軸、縦軸)のうち、一方の値はみなほぼ「0」で、点はほとんどが他方の軸の上に直線状に並んでいるという布置が得られています。
ここでは詳細割愛しますが、重み「0」の軸が生じ得るというのも、INDSCALモデルの大きな特徴です。
注1.因子分析は固有値分解を使ってはいても、こうした点に関しては、ほかの手法(主成分分析や対応分析)とは異なります。