7.クラスター分析(非階層的)
はじめに
全体を、指定した数に分割します。最低限でも、いくつに分割するかは分析者が指定します。
クラスタ初期値
クラスタ初期値は「ランダム」に決めるケースが多いようです(=分析者が指定しなくても良い)。データの傾向を適切に反映したクラスタ数を指定した場合であれば、クラスタ初期値はランダムでも、最終的にはだいたい同様の結果に落ち着くので、特に支障はありません。
他方、クラスタ初期値は決めてやることもできます。<クラスタ数×クラスタリングに使用している変数の数>の数値の行列を、クラスタ初期値として与えてやります。なお、「初期値」のため、通常は計算過程でデータに即してクラスタ中心は更新されて(移動して)いきます。ただし、適切な初期値であれば、結果は初期値と概ね似通います。
初期値を、ランダムに決めるか、指定するか → ※1
クラスタ内平方和の最小化
(ランダムであれ指定値であれ)とりあえずクラスタ中心の初期値が与えられたら、まず、ひとつの対象について、クラスターの数だけ、クラスタ内平方和を計算してみます。その結果、クラスタ内平方和(の増分)が一番小さかったクラスターに、その対象を所属させます。
これを全対象について行います。
全対象について、所属クラスターを計算し終えたら、あらためてクラスタ中心を再計算してみます。クラスタ中心は初期解からは移動しているでしょう。その場合、その再計算したクラスタ中心を使って、またすべての対象について、同様に計算していきます。
この計算結果に基づいて、またクラスタ中心を再計算します。クラスタ中心が移動するようであれば、また、再計算して、全対象をそれらの(新しい)クラスターに割り振ります。
これを何度か繰り返して、クラスタ中心が動かなくなれば、計算終了です。
クラスターの評価
このクラスタリングはうまくいっているのかどうか評価したいという場合もあるでしょう。K-means法では、「幾つに分けてくれ」と指定すれば、とにもかくにもその数に分けます。適切かどうかはさておいて。
分割数が最適かどうかは、基本的には、クラスタ内は似ていて、クラスタ間は似ていない、つまり、群内分散と群間分散(データにクラスタ番号を付与すれば、事後的に計算できます)を見ると目安になるでしょう。
ですが、総当り的に計算しても、群間分散の最大化、群内分散の最小化で最適なクラスタリングが見つかるというものでもありません(その場合、単純には、対象の数だけクラスターができます(ひとつひとつのクラスターに所属するサンプルはひとつ=群内分散は「0(ゼロ)」))。また、結果は、計算に使う変数ひとつ変えるだけで、簡単に変わるかもしれません。距離の定義でも変わりうるでしょう。特定の変数のスケールが変わっても結果は変わるでしょう。
他方、クラスタ中心を、あらかじめ指定することもできます。この場合たとえば、前もって,階層的クラスタリングを行った結果を使います。データが大きい場合は無作為サンプリングで小さなデータをいくつか作ってやれば良いでしょう。その結果から、クラスタ中心のデータを作ってやればこれを初期値とすることができます。サンプリングデータを作る場合、2,000ケースも対象があれば、大きなクラスタについては、意外と良く特徴が出ます。
クラスター分析(非階層的)の計算手続
- クラスタ中心の初期値を決める。
- すべての対象について、もっとも近い(クラスタ内平方和の増分が小さい)クラスターに割り振る。
- クラスタ中心を再計算する。クラスタ中心が移動すれば「2」へ。移動しなければ終了。
解釈
k-means法を使う場合は、データが目視するには大き過ぎる場合が多いでしょう(データが小さい場合は階層的方法を使うでしょう)。こうしたケースでは、結果をレーダー図で示すことが多いかと思います。例を挙げておきます(図表1.2.)。
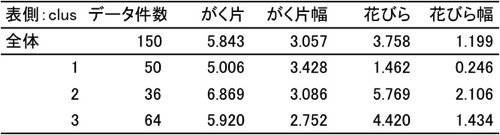
図表1.平均値表
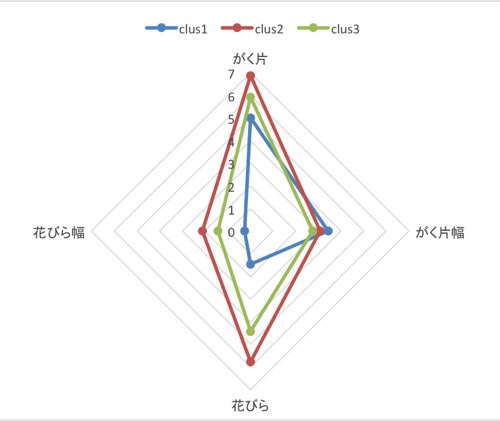
図表2.レーダー図
注1.階層的方法と、初期値をランダムに決めて計算した非階層的方法の比較を、下記に示します(図表3.)。
同じデータを、ward法で4クラスターに分けた場合と(グレーの線)、k-means法で4クラスターに分けた場合(カラーの線)を、MDS(ALSCAL)の結果(データは間隔尺度として計算。5次元解でRSQ=0.932。RSQ:もとデータから計算した距離とその推定値から計算した距離の相関を2乗した値)の付置(第1次元×第2次元)に重ねて表現した図です。
手法がいずれであるか(ward法/k-means法)で、4クラスターといっても、解は違います。ですが、付置(5次元解のうちの2次元で不完全ですが)と比べてみると、それぞれに、特におかしいというわけではないようです。
なお、ward法で4クラスターに分けた場合の各クラスターのクラスタ中心を計算して、それをクラスタ初期値として与えた場合、k-means法の4クラスタ解はward法の4クラスタ解と一致します(800ssほどのデータを使用しています)。
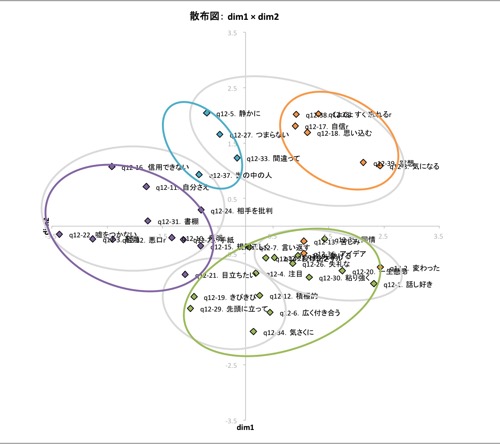
図表3.ふたつのクラスター分析の結果(グレーがward法,カラーがk-means法)

















