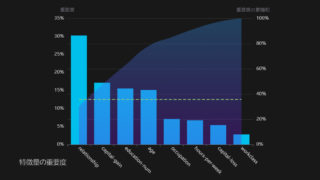
前回の記事では、『時系列データとその成分(ノイズ、周期性、トレンド)』について紹介しました。

この記事では、ベーシックな時系列分析の手法である、ARモデル、MAモデル、ARMAモデル、ARIMAモデルを紹介します。
ARモデルとMAモデルはARMA、ARIMA、SARIMAモデルなどの基礎にもなっている重要な時系列モデルです。
MA(移動平均; Moving Average)モデル
MA(移動平均)モデルでは、ある時刻のデータを「過去の時刻での誤差項」を用いて表現します。別の表現を使うと、過去の誤差を考慮しながらデータの推移を予測します。
ここで、q次のMAモデルをMA(q)と表すことにします。
まず一番シンプルな1次MAモデル、MA(1)を見ていきましょう。MA(1)は「現在の時刻は1つ前の時刻での誤差の影響を受ける」という考え方に基づいているます。
- 時刻の単位を「日」にした場合:「今日の値は1日前の誤差の影響を受ける」
- 時刻の単位を「秒」にした場合:「現在の値は1秒前の誤差の影響を受ける」
数式で表すと、下式のようになります。
yt = c + rt + θ1rt−1
この式からわかるように、データの特徴はパラメーターθの符号によって決定されます。
ここで、rtは時点tにおいて発生するホワイトノイズ(ランダムな誤差情報)です。MA(1)モデルは、現時点と1時刻前(t-1)までのホワイトノイズrt−1を使っています。
同じ式を使うと、時刻t-1に対する信号は、yt-1=c + rt-1 + θ1rt−2 と表現できます。そうすると、ytとyt-1の信号の間でrt-1という共通項を持つことが分かりますね。これは、ytとyt-1の間に「1次自己相関」が生じていることを意味します。
次に、q次のMAモデルMA(q)まで一般化すると、q時点前までの各時刻でのホワイトノイズを用いるので、下式のように表されます。
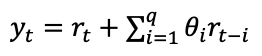
AR(自己回帰モデル; Auto Regressive)モデル
AR(自己回帰)モデルは、一定期間に遡る「過去の自分のデータ」を説明変数とします。そして、過去のデータに対し回帰を行うことで、現在の値を予測します。
数字で正確に説明すると、時刻tでのデータ値を、過去の時刻でのデータ(=過去の自分のデータ)yt-1, yt-2, …., yt-k を説明変数として回帰に使用するモデルです。
一番シンプルな1次ARモデルAR(1)は下式ように表されます
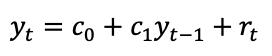
時点tにおけるデータが定数項、1つの時刻前のデータ、ホワイトノイズによって表されています。単回帰モデルとどこか似ている形です。AR(1)過程の性質はパラメーター c0とc1によって決定されます。c0とc1は回帰分析におなじみの最小二乗法で求めることができます。
自己回帰モデルは自己相関が存在するデータの場合にのみ成り立つものです。自己相関は、当日以前のデータの影響をどの程度受けているか(相関性があるか)を表すものです。上記の式においても、ytの式にyt-1の項が含まれているので、ytとyt-1が相関を持つことが分かります。
ARモデルは失業率などの経済指標や株価の分析など、時系列で変化する事象を表すデータに幅広く用いられています。
例えば、今日の株価は1日前の株価の値と相関関係がある場合、AR(1)過程と考えられます。1日前と2日前の2世代前までのデータと相関性がある場合にはAR(2)過程を用います。p日前までのデータと相関性がある場合にはAR(p)過程と呼びます。
このように、現時点よりも過去の実績値を説明変数(特徴量)として使用する場合、それらを特にラグ特徴量と呼びます。上記に株価予測の例では、「○日前の株価」はラグ特徴量にあたります。別の例でいうと、毎日の在庫数の変動を予測したい場合、ラグ特徴量は「○日前/去年・前々日の在庫数」や「ここ1週間の平均在庫数」などとなります。
では、q次のモデルAR(q)まで一般化すると、「現在の値」を回帰するためにi=1,2,…,q時点前までのデータを用います。この場合、q時点前までの各時刻での信号とホワイトノイズを用いて、下式のように表されます。
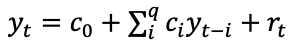
AR(q)の性質はパラメーター c0, c1,….,cq によって決定されます。これらも最小二乗法あるいは最尤法で求めることができます。
ARMA(自己回帰移動平均; AutoRegressive Moving Average)モデル
ARMA(自己回帰移動平均)モデルは、ARモデルとMAモデルを組み合わせたモデルです。ARモデルにMAモデルを加えたことでモデルの柔軟性が高まり、定常過程の時系列データに対して非常に強力な説明力・予測力を持っています。
ある時点の出力を、過去の出力と、現在および過去の入力に対する和で表現するモデルです。一般的に数学的にはARMA(p,q)モデルと記述されます。ここでpとqはそれぞれ自己回帰と移動平均の次数を表します。つまり、𝑝次ARモデルと𝑞次MAモデルであることを意味しています。
ARMA(p,q) の一般式は下式のようになります。
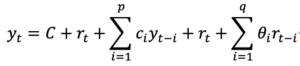
このように、ARMAモデルは現在の値を過去の値(yt-1, yt-2, …., yt-p)とホワイトノイズの和(rt-1, rt-2, …., rt-q)で表現されたモデルです。
ARMAを構成しているのはARモデルとMAモデルであり、MAモデルは常に定常性を有していますので、ARMAモデルが定常過程かどうかはARモデルが定常過程かどうかに依存します。
ARIMA(自己回帰和分移動平均; AutoRegressive Integrated Moving Average)モデル
ARIMA(自己回帰和分移動平均)モデルは、自己回帰モデル(ARモデル)、移動平均モデル(MAモデル)、和分モデル(Iモデル)を組み合わせたモデルです。
ある時点と直近時点の値の関係を分析し、それが将来も保存されると仮定します。予測精度がよく、非定常の過程も対応できるため、時系列分析手法の中では高い人気があります。
数学的に、ある時系列データに対して何度か差分を取った後に、データがARMAモデルで表現することが可能になります。 𝑑 階差分をとった系列に対してARMA( 𝑝,𝑞 )を考えるモデルをARIMA( 𝑝,𝑑,𝑞 )モデルと表現します。 つまり、時系列が ( 𝑑 次式のトレンド) + (定常部分) という構造である場合にARIMAモデルが有効といえます。
数式で表すと、下式のようになります。ARIMA( 𝑝,𝑑,𝑞 )モデルは時系列データのd階差分系列、𝑦𝑡 – 𝑦𝑡–𝑑をARMAモデルで表現するモデルです。
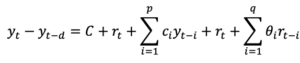
左辺はd階差分系列、式の右辺がARモデルとMAモデルの組み合わせ、つまりARMA(𝑝,𝑞)モデルであることが分かりますね。また、ARIMA(𝑝,𝑑,𝑞)モデルの3つの変数𝑝,𝑑,𝑞がそれぞれ𝑝次ARモデル、𝑑階差分系列、𝑞次MAモデルを表しています。
実は、ARIMAモデルは「汎用性の高いモデル」です。ARIMAモデルの3つの変数𝑝,𝑑,𝑞を変更することで、AR、MA、ARMAモデルを表現できることを確認してみましょう。
- 例:ARIMA(1,0,0)モデルは1次ARモデル
- 例:ARIMA(0,0,1)モデルは1次MAモデル
- 例:ARIMA(2,0,1)モデルは、ARMA(2,1)モデル
ちなみに、ARIMAの発展版にSARIMAモデル(Seasonal AutoRegressive Integrated Moving Average)があり、こちらはARIMAモデルに「季節的な周期パターン」を加えたモデルです。
いかがでしたか?
数式が出てきて大変な部分もあったかもしれませんが、上記を理解することで、時系列分析の基本的な考え方を身に付けることができます。
執筆担当:ヤン ジャクリン(分析官・講師)