時系列データとは
時系列データ(time series data)とは、広義的に言うと、時間の経過とともに変化するデータです。
時系列データは、ある現象の時間的な変化を測定することで得られます。測定の仕方として、連続的に値を記録するものもあれば、離散的に(つまり一定間隔ごとに)規則するものもあります。例えば、下図は一秒ごとに速度(rate)が変動する測定の結果を示しています。
ものすごく簡単に言うと、データをグラフ化したとき、横軸が「時間」なら、時系列データと言えます。
ただし、ポイントとして、一定の時間間隔で取得したデータであるという前提があります。 単純に取得したデータを時刻ごとに並べたものではなく、一定の間隔で取得していることを前提に取り扱う必要があります。
【時系列データの例】
- 音声、動画
- 毎日の気温や降水量
- 企業や店舗の売上推移
- 営業日ごとの株価の終値の変動
- 月ごとの飛行機乗客数
- 各種センサーの測定値(電流、電圧、温度、湿度、心電図、血圧など)
時系列データをうまく使えば、昨日の売り上げデータから、未来の売り上げデータを予測することができます。
時系列データの構造と成分
時系列データは複数の成分から成り立っています。データの値と時間の関係性を理解するために、各成分の特徴を把握することが重要です。
大きく分けて、ノイズ、周期性、長期トレンドの3種類の成分があると考えられます。以下では、時系列の変化を見る観点について紹介します。
■ノイズ
ノイズとは、分析したい情報や取り出したい情報を基準に、それらと関連しない全ての不要な情報であると定義づけることができます。別の言葉で言うと、説明変数に含まれる、目的変数と関係のない情報は、すべてノイズです。
理想な環境下でデータを取得することは難しく、ビジネスなど実世界で使われるデータには、かなり高い確率でノイズが紛れ込んでいます。分析モデルを構築する目的は目的変数と説明変数との間にある「真の関係」をモデル化することであり、もちろん真の関係の中にはノイズは含まれません。したがって、ノイズが混ざった状態で生データを使ってモデルを学習(モデルにフィット)しても、汎用的なモデルが得られません。
ノイズの影響を小さくするためによく使われる手段は、原系列の移動平均を取ることです。本記事の一番下で解説します。
■トレンド
トレンドとは一般的に、細かな変動やノイズを除いた、データ全体のなだらかな傾向を指しています。季節性の周期性の変動よりも周期が長いのです。
時刻が進むにつれて、観測値がどのような傾向を辿るのかを広範囲で捉えます。例として、気温の経年変化が挙げられます。月ごとや年ごとというよりも、何十年にも渡る上昇または減少の傾向を捉えるのがトレンドの視点です。
長期的な傾向を確認できれば、時系列データに対するモデリングに有用な情報が得られます。
■周期性・季節変動
データにおける周期性とは、一定時間ごとに繰り返される変動パターンのことです。季節変動はトレンドと比べ、周期が比較的短いことが特徴です。
- 例:オフィス街の喫茶店は週末に来客数が少ない(曜日の周期性)
- 例:冬に携帯用カイロの売上が圧倒的に高い(季節の周期性)
周期性の一種は季節変動の成分です。季節成分とは、主に、月ごとや四半期、一年など一定の間隔で繰り返される変動要因のことです。例えば、過去10年の日平均気温は、夏は高く、冬は低いので1年を通じて周期性が見られます。季節や気象の条件から影響を受ける商品、サービスを分析する際に必須な視点です。
季節変動以外の周期変動を周期性(循環変動)と呼びます。例として、景気指数変動に見られる好況、不況の繰り返しが挙げられます。
■短時的な変動、外れ値
季節変動やトレンドを取り除いた後に残る変動が短期的変動です。差分系列(隣り合う時の差)を取ることで抽出することができます。
差分系列に変換することで、長期的な変動が除去されて局所的な変動が明確になります。差分系列とは、時系列において前後の時刻の差分を計算して得られた系列です。
例えば、過去の数週間に渡って毎日の平均気温と前日の平均気温との気温差を可視化すれば短期的な変動が得られます。差分系列を取ることで、急激な変動による外れ値を見つけることもできます。
移動平均で平滑化
ノイズは分析の妨げとなり得る情報です。分析対象と無関係な成分を原系列から除いてはじめて本質的が見えてきます。そのために各成分(ノイズや周期性)の原因を確認しないと無意味な分析結果になります。
例えば、弁当の売上が好調な理由は
①メニューを改善した
②寒い天候が続き、外食から弁当購入に切り替えた人が多い
③ノイズによりたまたま売り上げが上がったように見える
このうち本当はどちらなのかを見極めたいときはありますよね。
ノイズや短い周期の変動の影響を小さくするためによく使われる手段は、原系列の移動平均(Moving Average)を取ることです。「平滑化」や「スムージング」とも呼ばれます。
移動平均とは、一定間隔で、連続して平均値を計算することです。下図のように、区間を事前に決め、区間を移動しながら平均値を計算し続ける処理です。
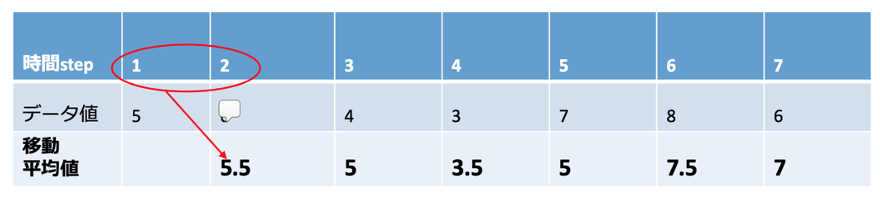
区間の範囲(間隔)は「窓」(Window:ウィンドウ)と呼ばれます。間隔を広く設定するとより長期的な変動を把握でき、細かい変化を掴みたい場合は間隔を小さめにとります。
時系列の移動平均を計算すると、移動平均系列が得られます(下図の赤い実線)。
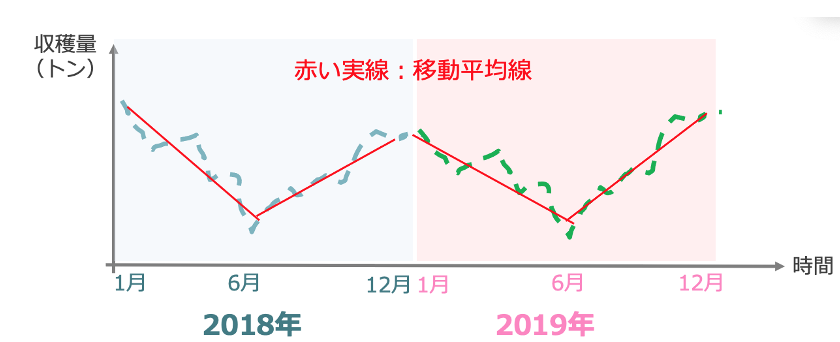
この処理によって、局所的な変動が小さくなり、細かな周期性の中にある長期的なトレンドを見やすくしてくれます。例えば、日ごとの平均気温のデータに対して移動平均を計算すると、季節の移り変わりによる気温の変動を可視化することができます。
この前処理を行うと、予測モデルの精度が向上することが期待できます。
しかし、やりすぎると、今度は本当に捉えたい傾向まで平坦にしてしまい、役に立たない結果となってしまいます。移動平均を計算する上でウィンドウサイズについては検討が必要で、ウィンドウサイズを大きくするとノイズの影響を小さくできる一方で、大きい範囲でのデータの傾向を見ていくことになり、一部の意味のある周期性パターンを見逃すリスクがあります。逆にウィンドウサイズが小さいときにはノイズの影響が残りやすくなります。 これを考慮しながら、バランスを取りつつデータの前処理をする必要があります。
次回は、時系列データの分析手法について解説していきます。
執筆担当:ヤン ジャクリン (分析官・講師)
















