3．因子分析（直交回転）
はじめに
（複数の）変数の背後にある、抽象的な概念（潜在変数）を探し出します。測定されている変数は、測定されていない潜在変数から影響を受けていると考えます。
因子は“ある”ことが前提（主成分分析との比較）
心理学分野をはじめとして、因子分析はしばしば使われています。しかし、この分析はとても不思議な分析です。主成分分析と、ちょうど矢印の向きが逆（パスが逆向き）です。このあたりは図で見る方がわかりやすいでしょう。
図表1．が主成分分析、図表2．が因子分析です。
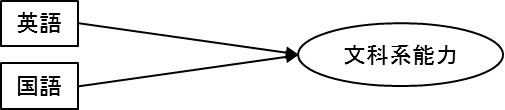図表1．主成分分析の例
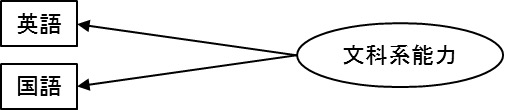図表2．因子分析の例違う点はひとつ、矢印の向きです。
直接測定できるもの（観測変数）は、「英語」「国語」です。「文科系能力」は直接測定しているのではありません。ここでまた違いが出るのですが、「文科系能力」は、主成分分析では合成変数、因子分析では潜在変数となります。両者には、共通性が1かそれ未満か、といった違いがあるのですが、この点はここでは触れません。それよりも矢印の向きの違いに着目します。
主成分分析か因子分析かでパス（矢印）の向きが真逆です。
「英語」の点数、「国語」の点数がまずあって、それらを合成して作るのが「文科系能力」、という話の流れが主成分分析。
「文科系能力」がまずあって、「英語」の点数、「国語」の点数は、その「文科系能力」の実現値として、実際に測定できる形で得られる、という話の流れが因子分析。
理屈としては、まず「文科系能力」というものがある。ところがそれを直接測ることができない。だから「文科系能力」から影響を受けている「英語」や「国語」を測る、という筋道が因子分析です。
非常に良く使われているのですが、こういう筋道で成り立っている手法なのだ、ということも念頭にあっても良いのではないでしょうか。
少ない潜在変数からたくさんの顕在変数に
顕在変数の背後にある潜在変数を見つけ出します。測定できない変数（潜在変数）があって、これが測定できる変数（顕在変数）に影響を与えている、という構図を考えます。
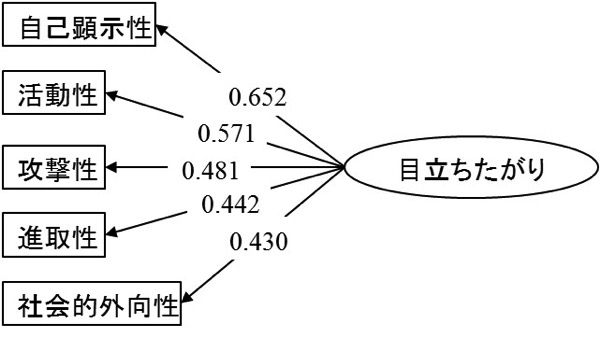図表3．潜在変数から顕在変数へのパス図表3．では、「目立ちたがり」という潜在変数があって、これが「自己顕示性」や「活動性」……といった顕在変数、すなわち性格的特性の測定値に影響を与えている、という状況を表しています。パス（矢印）に書かれている数字は影響の度合いです。（基本的に）「1」～「-1」の値をとり得ます。
「自己顕示性」や「活動性」……は、直接測定できる顕在変数です。たとえば、アンケートの回答に基づいて計算します。他方、「目立ちたがり」の方は潜在変数です。直接測定することはできません。手元にある顕在変数（「自己顕示性」など）の値をもとに、分析者が恣意的に指定した観測変数と潜在変数の関係に基づいて（作業上は因子数を指定するだけだったりしますが）計算されます。
共通性（と独自性）
以下、図表3．に沿ってみていきます。
潜在変数（「目立ちたがり」）が先にあります。顕在変数としては「自己顕示性」「活動性」……などありますが、どの変数も完全に「目立ちたがり」と連関があるのではありません。たとえば「目立ちたがり」から「自己顕示性」へのパスには「0.652」とあります。「自己顕示性」は「目立ちたがり」から「0.652」影響を受けています。「自己顕示性」のうち、「1」から「0.652」を引いた「0.348」 は、「目立ちたがり」から影響を受けていない、「自己顕示性」独自の部分ということになります（「目立ちたがり」だけに関して言えば）。
通常、潜在変数にも複数の因子を想定するので、話はもう少しだけ複雑ですが、仮に一因子だけで考えると、「自己顕示性」は「目立ちたがり」との間に「0.652」の共通性があり、「0.348」の独自性がある、ということになります。
因子分析の計算手続
因子分析は、少しステップが多くなっています。大雑把に言って、以下のような手順を踏みます。まずは直交回転についてみてみます。
【計算のステップ】
0．相関係数行列の計算→1．固有値分解→2．因子数の決定→3．固有値分解→4．因子負荷量の計算→5．因子負荷量の回転→6．因子負荷量の2次元ソート→7．因子の解釈
あらためて、それぞれ簡単に内容を見ていきます。
0． 相関係数行列の計算
因子分析では、分散共分散行列は扱いません。相関係数ですので、対角は「1」です。
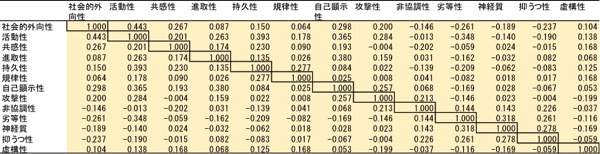図表4．相関係数行列1．固有値分解
相関係数行列を固有値分解します（＝主成分分析）。たとえば10次元以上まで求めます。
図表5．固有値／寄与率／累積寄与率それにより得られた10個以上の固有値を使って、スクリープロット（崖状の図）を描きます。（図表6．）
2．因子数の決定
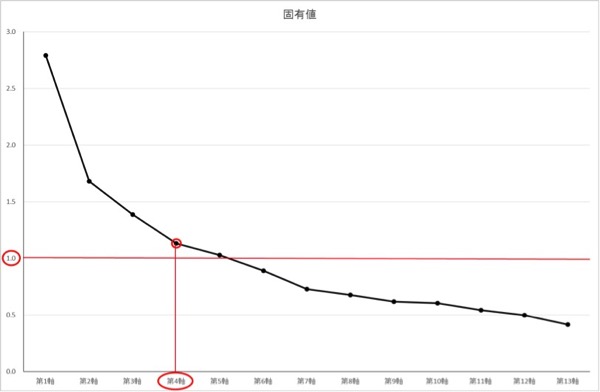図表6．スクリープロットスクリープロット（崖状の図）を見て、因子数を決定します。「肘の基準」と称しますが、傾きが小さくなる前までの次元数を採用します。通常は固有値が「1」を上回る範囲から選びます。上記（図表6．）では4次元でしょうか。
3．固有値分解
相関係数行列の対角部分（全部「1」）を共通性で置き換えて、再度固有値分解をします（因子分析）。共通性は、簡単には、推定したい変数をそれ以外のすべての変数で予測した場合、どれだけ予測できたか、その程度を表します（SMC）。（図表7．のように共通性（の初期値）が低い場合は、使用する変数を再考する方が良いかもしれません）
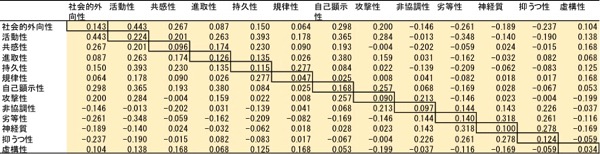図表7．対角にSMCを入れた相関係数行列（多くの場合共通性は反復推定します）4．因子負荷量の計算
元の相関係数行列の対角要素を共通性で置き換えた行列を固有値分解します（通常は共通性を反復推定するので少しややこしいのですが）。求まった固有ベクトルの値に、求まった固有値の平方根（特異値に相当）を乗じて、因子負荷量（主成分分析の場合の主成分得点に相当）を求めます。
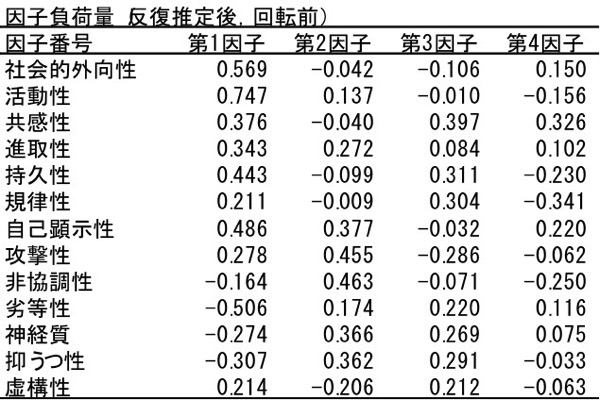図表8．因子負荷行列（回転前）5．因子負荷量の回転
求まった因子負荷量を、解釈しやすいように回転します。たとえば「バリマックス回転」が使われます。これはその名の通り、バリアンス（分散）がマックス（最大）になるように回転します。回転により解釈しやすくなります。
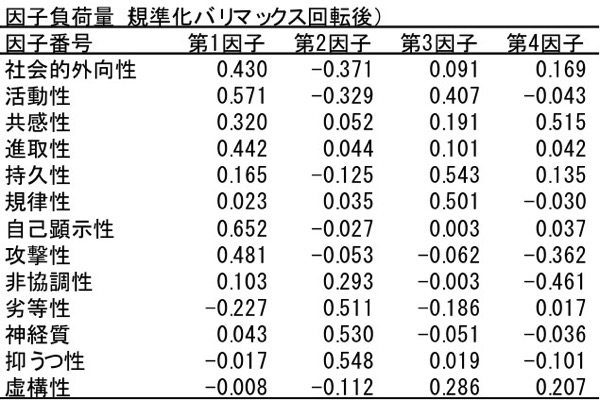図表9．因子負荷行列（回転後）6．因子負荷量の2次元ソート
回転した因子負荷行列を、2次元ソート（各変数とも最も負荷量の絶対値が大きい次元について、負荷量の絶対値の大きい順に並び替える）します。単に表の見やすさの問題ですが、並び替えないと、解釈には相当な手間がかかるかと思います。
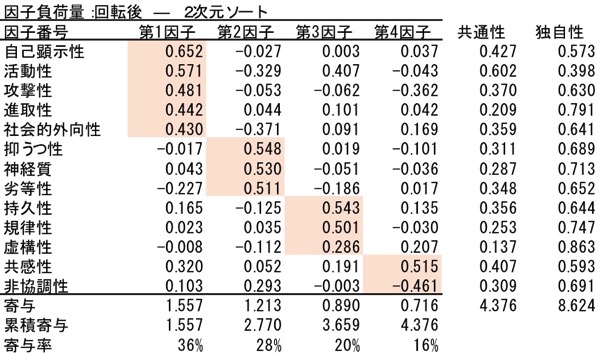図表10．因子負荷行列（2次元ソート後）7．因子の解釈
ようやく分析結果の解釈です。2次元ソートした因子負荷量（図表10．）を解釈します。具体的には、潜在因子に名前を付けます。これは具体的な例を次に示します。
解釈
そもそも因子分析では、因子数はこちらが指定した数であることを前提にします。たとえば4因子を指定したのならば、5因子以降が表現している情報は、当該の分析とは無関係の情報として無視します。共通性があるので（「1」未満なので）目安程度（正確ではない）ですが、主成分分析の結果の4軸までで表現している54％ほどの情報しか使っていない（このデータの46％は因子分析に使われていない）ということは、まず見ておいて良いと思います。
因子寄与（各次元がどれだけの情報を持っているのか）は、通常あまり気にする必要はありません（回転するとある程度なれるため）。ただ、あまり極端に違う場合は、念頭に置いて解釈するか、あるいは（あまり寄与が小さい軸がある場合）指定した因子数が、そもそもおかしかった（データと合わない）、あるいは顕在変数として測定した変数は、想定した因子構造とはあまり関係がなかったのかもしれません。
そのほか、解釈にあたっては以下の2点にも気を付けて見てください。
1点目。解釈は、因子負荷量の絶対値が大きい項目に着目して行います。つまり、因子負荷量の絶対値が小さい場合あまり気にしません。因子負荷量は、因子と顕在変数との相関係数だと思ってください。シンプルには、あまり関係がない（値の絶対値が小さい）顕在変数は、あまり気にしないでもいいでしょう（たとえば第1因子の虚構性）（ほかの変数をひとつ外すと、急にほかの顕在変数の負荷量が大きくなったりする場合もあるので一概には言えません。そもそも因子負荷量が小さい項目があること自体が望ましい状態ではありません）。
2点目。同じようなことが共通性（独自性）についても言えます。解釈は、共通性が大きい顕在変数に着目します。独自性（1-共通性）が大きい顕在変数はあまり気にしないでも良いかもしれません（たとえば虚構性）。
因子分析の解釈は、主要には因子に名前を付けることで行います。
因子に名前を付ける。たとえば図表10．の4因子だと、以下のような感じでしょうか。
第1因子：目立ちたがり
第2因子：内気
第3因子：タフさ
第4因子：なかま意識
