統計学の2つのアプローチ
統計分析の２つの主要なアプローチは記述統計学と推測統計学です。両者には、「全データを対象とするかどうか」それとも「母集団から標本を抽出して標本を分析の対象とするか」などのような違いがあります。
記述統計学は昔から活躍してきた学問分野であるのに対して、推測統計学は1920年代に発生した比較的若い学問分野です。
■記述統計学（descriptive statistics）
手元にあるデータの特徴や傾向をわかりやすく・直感的に説明するを目指します。具体的に、データを整理し、基礎統計量（平均や分散など）を算出し、表やグラフで可視化します。記述統計学は手元のデータを「全対象」と解釈します。したがって、分析対象のうちデータを収集できないものがある場合は、原則として記述統計学で扱うことができません。
■推測統計学（inferential statistics）
データ全体（母集団）から一部（標本）を抜き出して、その標本の特性を調査することによって、母集団の特性を推測します。さらにその推測が正しいかどうかを、統計的な手法および確率の考え方を用いて検定します。
この記事では、記述統計学に対する推測統計学の特徴に着目しつつ、推測統計学がどのように活用されているのかを見ていきましょう。
記述統計学の弱点とは
記述統計学を活用することで、基礎統計量を算出し可視化することで、手軽に、効率よくデータの特徴を表現できます。一方で、記述統計学が適していない分析がたくさんあります。記述統計学は基本的に「全数調査」であるため、完全なデータを全て取得できない場合は難しいといえます
例えば、菓子メーカーがマーケティングに施策を打つために、お店が位置する地域の全ての世帯が菓子類に費やす１ヶ月の金額の平均を知りたいとします。
このケースでは、以下をクリアしないといけません。
地域の全ての世帯に対して、菓子類の出費のアンケート調査を行い、漏れなく回答を回収する
全世帯から回答を回収するだけでも相当難易度が高いのに、実はもっと厄介なハードルが潜んでいます。アンケート回答を全部回収できたとしても、入力不備（未回答や趣旨外れの内容）が含まれる可能性もあります。地域全体に対する調査なので当然データ量は膨大に膨らみます。このデータに不備の有無を確認しながら集計することは非現実としか言えようがありません。
まとめると、「地域の全ての世帯に関する完全な回答」を確実に回収できる見込みがないため、（厳密にいうと）記述統計学を用いて「菓子類に費やす１ヶ月の金額の世帯平均」を求めることが不可能です。この課題を克服できるのは、次に解説する推測統計学です。
推測統計学の特徴
前述の通り、記述統計学は全データの収集が不可能な場合、あるいは、調査データの量が大きすぎる場合に使いづらくなってしまいます。このような場合、推測統計学を使用できます。推測統計学は、名前に「推測」があり、名前の通り、以下のアプローチをとります。
集団から抽出した一部から集団全体の性質を調べ、その結果に基づいて元の集団全体の性質を「推測」する
統計学の用語では、集団全体を母集団と呼び、母集団から抽出した一部のデータを標本（サンプル）と呼びます。
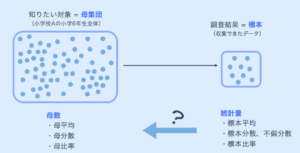
推測統計学における考え方の大まかな流れは以下となります。
- 母集団から標本を集める。このプロセスは「サンプリング」と呼ぶ。
- 標本データの特徴を把握する。
- 標本に対して調査や処理を行い、その結果にもとづいて、「母集団はこういう分布をしているのであろう」という仮説（モデル）を立てる。
- 上記の仮説が正しいかどうかを統計学的な手法を用いて検証する。
推測統計学の使用例
推測統計学は実に応用の幅が広い分野です。2つの主な分析手法は「統計的推定」と「統計的仮説検定」です。これらの考え方は、確率や確率分布に基づいています。
ここではまず、「推計統計学を使ってどんなことができるのか」についてイメージを持ってください。以下に応用例をいくつか書きました。括弧に書かれているのは具体的な統計分析の手法です。
- 選挙の出口調査、テレビ番組の視聴率（統計的推定）
- 新規開発された治療法の有効性（統計的仮説検定；t分布を用いた２つのデータ群の差の検定）
例えば、テレビ番組の視聴率の調査では、全世帯に対して「番組を見たかどうか」を調査することは不可能です。代わりに、一定数の世帯を（出来るだけ偏りなく）抽出し、（視聴率をモニターする装置を設置し）「番組を見たかどうか」を調べ、その結果に対して「統計的推定」の手法を用いて、テレビ番組の視聴率を推定します。
この例では、母集団は全世帯、標本は調査した一定数の世帯です。
標本を用いた推定はどれくらい正しい？
では、統計学的に推定した結果がどれくらい正しいのかをどうやって知ることができるのでしょうか？
推測統計学が使用されている「選挙速報」は、すべての開票が完成する前に開票結果を予測するために実施する「出口調査」の結果に基づいています。この場合、推定の正しさが検証することは可能です。全開票後の最終的な結果と比べればいいだけです。正式の全開票は母集団の全数調査（記述統計学）が使われています。各党についてのパーセンテージが完全に一致することはなかなかないのですが、少なくともどれくらい正しい（近I）のかを評価できます。
一方で、世の中ではほとんどの場合、標本調査の結果が本当に母集団の特性を代表できているのかを厳密に検証できません。上で挙げた「テレビ視聴率」の例において、全世帯を調べることは実質上不可能なので、
「テレビ視聴率」は「おおよそ34%」のように、推定結果として1つの値を出力しています。結局、この推定結果の1つの値が正しいかどうかを知る術がありません。
代わりに、「値の範囲」を推定し、かつその推定が正しいと思われる確率も扱うやり方があります。これは次に話す「区間推定」です。
点推定と区間推定
統計的推定には点推定と区間推定の２種類があります。
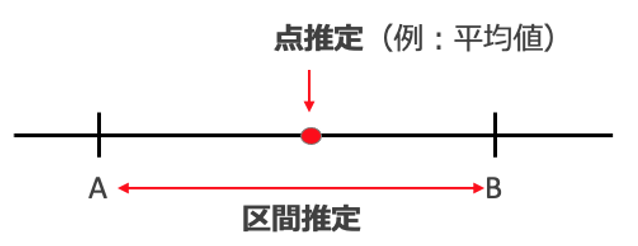点推定の場合は１つの母数の値を推定し、区間推定の場合はある信頼度をもって母数が入る区間[A,B]を推定
「点推定」とは、母数を１つの値で推定することです。例えば、標本平均（１つの値）で母平均を推定することや標本分散（１つの値）で母分散を推定することが点推定です。
ところで、上の図の赤い点のように、１つの値だけで推定した母数値はどれくらい信頼性があるのかを思う方もいるでしょう。
「区間推定」とは、標本を用いて母数が存在しうる区間を推定することです。この時、「推定した区間に母数が実際に収まる確率」を考えることが重要です。この確率値を一般的に「信頼度（信頼水準、信頼係数）」と呼びます。信頼度によく使われる値は 90%, 95%, 99%です。
また、信頼度に応じて推定した結果を「信頼区間」と呼びます。
先ほどの「テレビの視聴率の調査」の例では、もしも「番組Aの視聴率は34%と思われる」という推定は点推定にあたります。これに対して、区間の幅を持たせて「信頼度95%をもって、番組Aの視聴率は28%〜40%と推定する」という推定は区間推定にあたります。
執筆担当：ヤン ジャクリン （分析官・講師）
