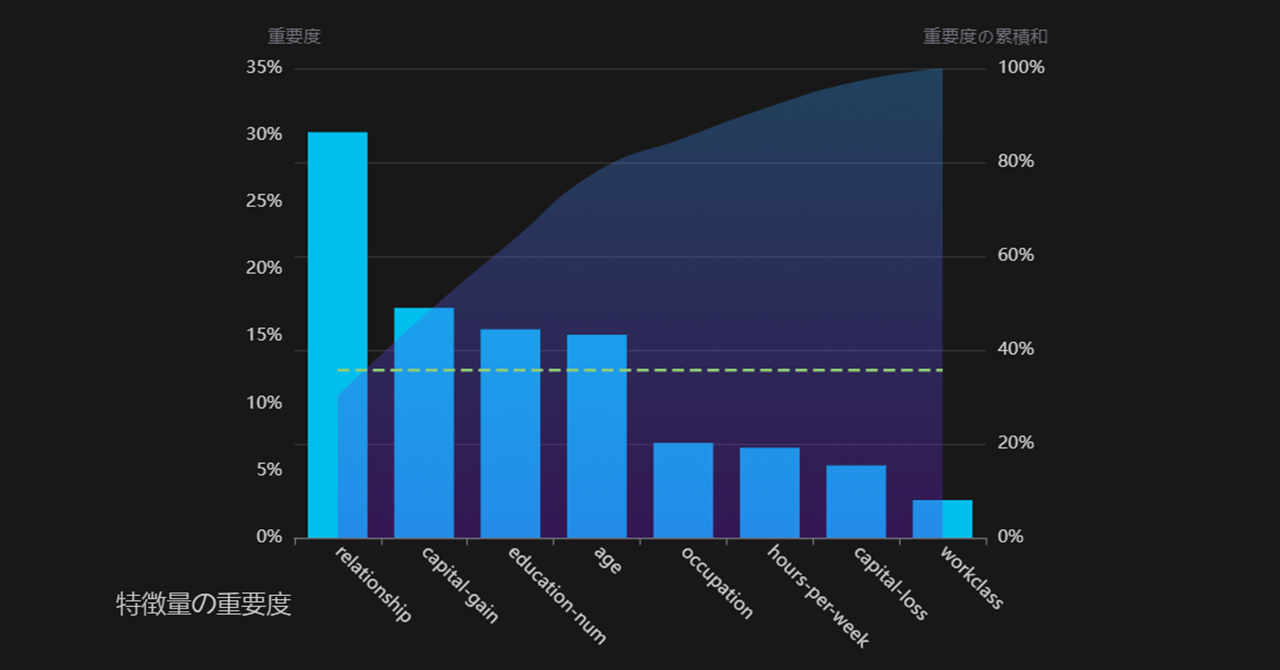
t検定はなぜよく使われる?
統計学に基づいた仮説検定の中でよく用いられる手法の1つはt検定(t-test)です。
t検定は、t分布を利用する統計的仮説検定です。t分布は正規分布と深い関係性があります。実際、t検定は母集団が正規分布に従うと仮定した上で実施します。
t検定がよく使われる理由は以下と言われています。
- 母分散が未知であることが多い→z検定を使えず、t検定は使える
- 標本サイズが小さくても、使える
ポイント①に関して: t検定とz検定は両方とも正規分布と関係性が深く、扱う標本データが正規分布に従うと仮定しています。両者の違いの1つは、母分散に関する情報が必要かどうかにあります。z検定は、正規分布の母分散が既知であるときにのみ利用できる検定手法です。これに対して、t検定は母分散未知の正規分布に従う場合の検定手法として使われます。
実世界では、ある現象が正規分布に従うとわかっていても、その分布の母分散が知られていないことが最も「普通」の状況です。その場合、救済処置として(理論上は完璧に正しくないが)実用上、母分散を標本分散で代用してz検定を使うことがあります。ただし、これが許されるのは、標本サイズが十分に大きい時のみです。標本サイズが、10や20のように小さい時は標本分散で代用不可になります。そうすると、正規分布に依存するz検定は使いものにならなくなります。
この場合は、正規分布の代わりにt分布、z検定の代わりにt検定を使います。これがポイント②に結びつきます。
以上より、t検定はz検定よりも汎用的と言えます。
t検定は、マーケティングなどビジネスの場面、自然科学など分野横断的に非常によく使われます。「何かをした後に差が出ているかどうか」を調べるのが代表例です。例えば、マーケティング活動の中で、「販促キャンペーンの効果があったのか?」や「2種類の顧客層の間に来店回数に差があるのか?」を調べるときに使います。
数値を見るだけで、そのままの意味での「差」があるかどうかはもちろんわかりますが、これが統計学的に有意かどうかは仮説検証を使わないといけません。
t分布の特徴は?
下図には、自由度1,3,15,100のt分布の密度関数のグラフが示されています。t分布の自由度が大きくなるにつれ、標準正規分布のグラフに近づくことが分かります。
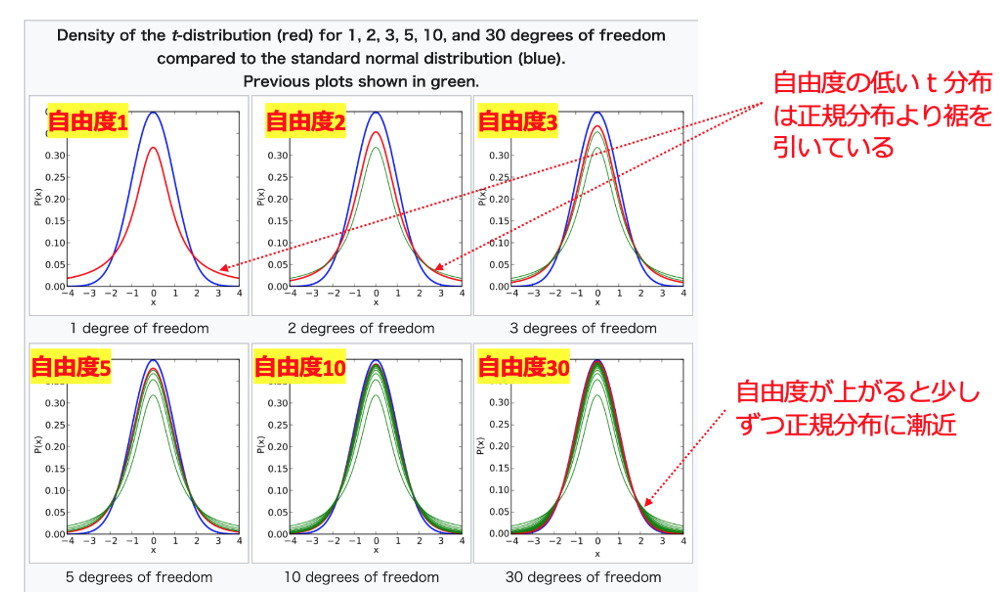
t検定と正規分布の関係性について2つのポイントがあります。
- 自由度が大きくなればt分布は正規分布に漸近する
- 小さな標本がt分布に従う場合でも、その母集団が正規分布に従うという仮定が必要
以下では、もう少し数学的に説明します。
t検定の典型的な応用例は、「独立な2標本の平均値の差の検定」です。
ここでは、グループ1とグループ2の、正規分布𝑁(μ,σ2)に従う2つのデータ群から、無作為抽出された標本データがあるとします。それぞれのデータサイズがn1, n2 だとします。また、標本データから計算された平均がそれぞれx1, x2、不偏分散がそれぞれ、S1^2, S2^2になったとします。
この場合、t-統計量は以下の式のようになります。
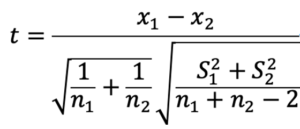
z検定と違って、t検定量は分母に不偏分散を用いることがポイントです。
これは何を意味するかというと、正規分布に従うと仮定した標本について、分散を不偏分散によって標準化すると、自由度n-1のt分布に従うということです。母分散が未知でも、不変分散を用いて、t分布に標準化して行うのがt-検定です。
この例のように、比べている2つの集団のデータサイズと不偏分散が異なる、というのが最も汎用的なケースを考えます。一方で、不偏分散が等しいと仮定した上で小標本の場合を扱うこともあります。
この後、実際の数値を使ったt検定の演習を一緒にやっていきますが、その際に必要なのはt分布表です。t分布表とは、t統計量がt-分布における任意の「限界値」以上の値をとる確率を、一覧にしたものです。
t分布表は様々な資料で見つけることができます。例えば下が一例です。
https://bellcurve.jp/statistics/course/8970.html
t検定ではt分布表を頻繁に参考にするので、その見方を演習問題でマスターしましょう。
t検定を実践しましょう
下図は自由度10のt分布を用いて、有意水準5%を設定した場合のt検定の模式図です。
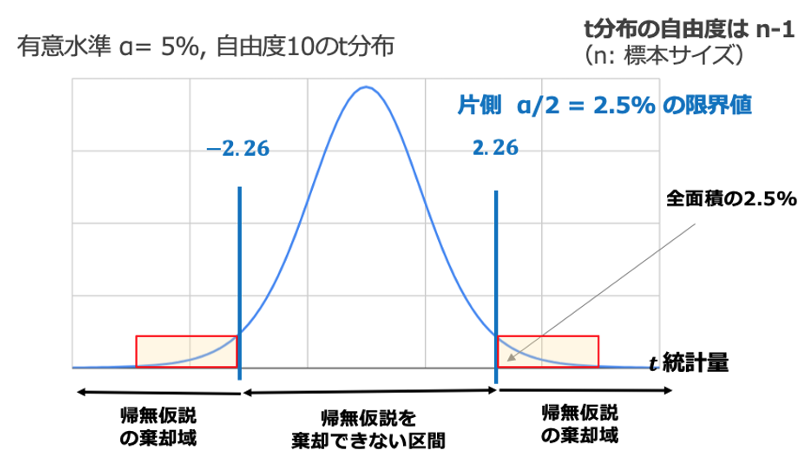
t分布の形とz分布(正規分布)の形を見比べると、t分布の場合、帰無仮説の受容領域はz分布よりも広いことがわかります。また、t分布は自由度が小さくなどほど形がとんがっているので、自由度が小さくなるほど帰無仮説を棄却しにくいことがわかります。
t検定の例題:新開発の薬の効果を検証
ここでは、以下を有意水準5%で検定するケースを考えます。
「新開発の薬に患者の病状を改善する効果があるか」
この仮説検証のために以下のように実験を行います。
- {集団1:薬を投与した患者}と{集団2:薬を投与しなかった患者}のそれぞれから無作為で抽出した経過観察データを標本とする
- 経過観察データにおいて、検定の対象とする測定値が高いほど病気の症状が顕著である
- 集団1、集団2のデータサイズ、と測定値の平均、不偏分散は以下である
- 「未投与」 n1=10名 測定値: 平均 x1 = 38 不偏分散 S12 = 82
- 「投与」 n2=20名 測定値: 平均 x2 = 30 不偏分散 S22 = 62
仮説は以下となります。
帰無仮説:
![]()
対立仮説:
有意水準5%の片側検定を使用します。
では、 t検定量を計算します。t検定量の式にデータサイズ、と測定値の平均、不偏分散を代入すると結果は以下となります。
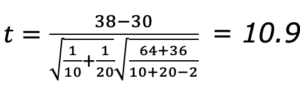
自由度 28、信頼区間5%の値をt分布表の片側検定を読み取ると1.7程度です。上記のt検定量はそれを超えているので帰無仮説を棄却できると判断します。
従って、新しく開発された薬は効果があると認められます。
実際、自由度(データサイズ)が28程度だと、ほぼ正規分布を使うのとあまり変わりません。
いかがでしたか?
この記事により、t検定の使いやすさや実際のイメージを把握できたでしょうか?是非身近のデータに対して使ってみてください。
執筆担当:ヤン ジャクリン(分析官・講師)