概要
この記事では、トポロジカルソートと呼ばれる手法によるタスクの順序付けを解説します。
例えば、食事の準備を考えます。朝食に鮭を焼き、一部をお弁当のおにぎりの具にするといった具合です。
この作業についてタスクの関係は以下のような図で表現できます。
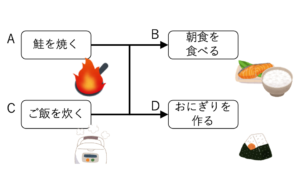
ここで、例えばAからDへの矢印は鮭を焼いておかないとおにぎりが作れないことを示しています。つまり、BとDを実行するためには、AとCを先に実行しておかないといけないという訳です。でなければ食中毒を起こしてしまいます。
さて、これは規模が小さい例なので直感でタスクの順序を見つけることができます。
しかし、より規模が大きく複雑な依存関係を持つタスクが現れたとき、直感では太刀打ちできません。機械で自動的に手順を見つけるにはどうすればよいでしょうか。
ここでは、そのために利用できるアルゴリズムを説明します。
トポロジカルソート
できること
トポロジカルソートは、DAG(有向非巡回グラフ)と呼ばれる類のグラフについて一定の順序付けをする手法です。
実は先程の図はDAGの仲間になっています。
DAGにおける有向はAを実行しないとDが実行できないという関係、非巡回はA→D→A→D→…のようなループする関係がどこにも存在しないことだと言い換えることができます。
さて、トポロジカルソートを行うことで、ABCDを一列に並べることができます。
そして、その並び方にはルールがあります。
どのタスクもそこから伸びる矢印の先のタスクより必ず先にくるように並ぶというルールです。
このように並び替えて先から実行することで、生鮭を食べるというようなミスを避けられます。
このようなルールを満たすような並び方は複数ありますが、例えばA, C, B, Dと並びかえられます。
A, CがB, Dよりも先に来ているのでこの順序で実行すれば問題有りません。
方法
では、どのようにすれば機械的にトポロジカルソートを行えるでしょうか。
その方法の一つ*を紹介します。
*Topological sorting of large networks
それは、先に終わらせるべきタスクが存在しないものから先に列に追加していくというアルゴリズムです。
今回の例では、まずAとCが条件に当てはまります。
AとCはどちらが先でも構いませんが、まずAを選び列に追加します。
そして、AとAから伸びる矢印を削除します。
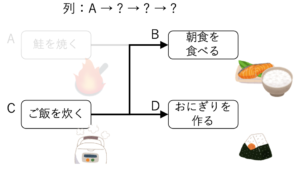
Cについても同様の操作を行います。
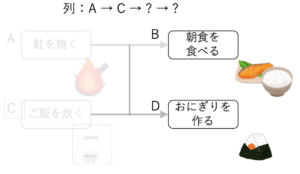
こうすると、BとDが前述の条件を満たすようになります。
そのため、同じ手順を繰り返すことでBとDを列に追加することができます。
結果として、A→C→B→Dという順序を得ることができました。
終わりに
今回はトポロジカルソートの解説をしました。
扱った例では、所要時間や締切などの概念がありませんでしたが、そのような概念を取り入れた場合にどうなるか考えるのも面白いと思います。
ちなみにPythonでも3.9以降ではトポロジカルソートのためのクラス*が組み込まれているようなので、試してみたいです。
*graphlib — Functionality to operate with graph-like structures
















