スピアマンの順位相関係数とは
一般的に相関係数と知られているものは「ピアソンの積率相関係数」とも呼ばれています。これは、量的データに対して、2変数の直線的な相関関係(線形関係)の強さを表す指標です。
しかし、2変数の間で線形な関係が存在しない場合やデータの値の順位しか情報がない場合には、「ピアソンの積率相関」を適用できません。
そんなときに、スピアマンの順位相関係数が有効に使われます。量的なデータを順位付けし質的データに変換した上で、2つの変数の単調関係を表すのに使われます。ここで、「単調関係」とは、一方の変数が増大(減少)するともう一方の変数が増大(減少)するような関係性を指します。増加または減少の量的な評価をしなくて良いのです。
大学の統計学の授業で、なんとなく習った記憶がありますが、社会人になってからその知識を応用する機会がないまま今日まで来ました。執筆者も本記事の中で手を動かして計算することで、自分の復習も行なっています。
さて、本題に入ります。
図1の左と右の散布図を比べてみてください。
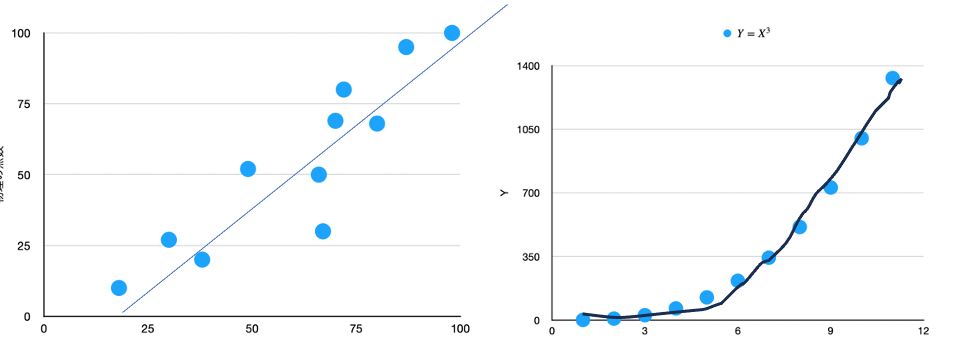
図1:(左)2変数の間の線形な関係があり、ピアソンの積率相関が適用される。 (右)2変数の間の非線形な関係があり、スピアマンの順位相関が適用される。
左は、データの点がほぼ直線上に並んでいます。これらのデータに対して、ピアソンの積率相関係数を計算することができます。右の方のデータは曲線 y = x3 の上に並んでおり、XとYの変数間に非線形な関係があります。YがXに対して単調増加しているので、スピアマンの順位相関係数の符号はプラス(+)です。
スピアマンの順位相関は量的データを順位に変換しているだけなので、値の増加の幅を考慮せず、単調増加または単調減少するかどうかにのみ注目します。
スピアマンの順位相関係数を計算してみましょう
では、スピアマンの順位相関係数を実際に計算してみましょう。
表1には、8名の顧客による商品Aと商品Bの評価スコア(1と10の間の値を取り、10が一番良い)のデータが示されています。このデータを用いて、スピアマンの順位相関係数の求め方をみていきましょう。
商品Aに良い評価を与えた顧客が商品Bにも良い評価を与えるのか、それともその逆で悪い評価を与えるのかをある程度この分析から知ることを目指します。
| 顧客_id | 商品Aのスコア | 商品Bのスコア |
| 1 | 8 | 7 |
| 2 | 2 | 1 |
| 3 | 4 | 4 |
| 4 | 6 | 4 |
| 5 | 6 | 5 |
| 6 | 5 | 3 |
| 7 | 9 | 8 |
| 8 | 10 | 7 |
表1:8名の顧客による商品Aと商品Bの評価スコア(1と10の間の値を取り、10が一番良い)のデータ
まず、スピアマンの順位相関係数は式1で計算されます。
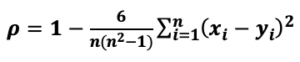 ….式1
….式1
ここで、nは2つの変数のデータの数、x_iとy_iはi番目のデータにおけるそれぞれの変数の順位です。係数は2変数の順位の差分(x_i – y_i)に注目して計算されます。
「スピアマンの順位相関係数」は「ピアソンの積率相関係数」と同じく、-1と1の間の値を取ることができます。⍴値を0に近づけると、2つのランク間の関連付けが弱くなります。
- ⍴値が1に近い:2変数間で順位の正の関連付けが強い
- ⍴値が0に近い:2変数間で順位の関連付けがほぼない
- ⍴値が-1に近い:2変数間で順位の負の関連付けが強い
Step1:データの順位付け
一方の変数を増やすと、もう一方の変数が単調な増減の関係に従うかどうかを観察することがポイントです。よって、スピアマンの順位相関係数を計算する前に、データを順位付ける必要があります。
表1に順位をつけたものが表2です。
最大の値を1位にするか10位にするのかはほとんどの場合どちらでもよいです。ただし2変数で共通の規則を適用することが重要です。ここでは、ベストのスコアを順位1とします。
同じ値がある場合には、「中間の値」を取るように同じ順位が振られるよう補正を加えます。例えば、顧客id4番目と5番目の商品Aのスコアの順位は (4+5)/2 = 4.5 です。ところが、データ数が多すぎる場合は、いちいち目視で中間の値を計算するのが大変なので、ExcelのRank.Avg関数を利用して処理すると効率的です。
| 顧客_id | 商品Aのスコア順位 | 商品Bのスコア順位 |
| 1 | 3 | 2.5 |
| 2 | 8 | 8 |
| 3 | 7 | 5.5 |
| 4 | 4.5 | 5.5 |
| 5 | 4.5 | 4 |
| 6 | 6 | 7 |
| 7 | 2 | 2.5 |
| 8 | 1 | 1 |
表2:表1のスコア評価に順位をつけた結果。
Step2:2変数の順位の偏差の計算
次に、2変数の順位の差およびその2乗を算出します。これは式1で使用するためです。その結果は表3に示されています。
| 顧客_id | 商品Aのスコア順位 | 商品Bのスコア順位 | 順位の差分 | 順位の差分の2乗 |
| 1 | 3 | 2.5 | 0.5 | 0.25 |
| 2 | 8 | 8 | 0 | 0 |
| 3 | 7 | 5.5 | 1.5 | 2.25 |
| 4 | 4.5 | 5.5 | -1 | 1 |
| 5 | 4.5 | 4 | 0.5 | 0.25 |
| 6 | 6 | 7 | -1 | 1 |
| 7 | 2 | 2.5 | -0.5 | 0.25 |
| 8 | 1 | 1 | 0 | 0 |
表3:
Step3:スピアマンの順位相関係数の計算
表3の5つ目の列の偏差の2乗、および式1を用いて、スピアマンの順位相関係数は以下のように計算されます。
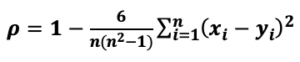
= 1 – 0.0119・5
= 0.9405
上記で計算されたものが1にかなり近いです。これにより、商品Aと商品Bの顧客による評価の間には、順位の関連度合いが高いことがわかります。
執筆者:ヤン ジャクリン (GRIデータ分析官・講師)
















