時系列データをトレンド、サイクル、季節、残りの各要素に分解する手法についてまとめていきます。
なお、こちらの記事を参考にしています。
時系列データは加法モデルを用いると一般的に以下のように表されます。
$$y_t=S_t+T_t+R_t$$
ここで、$y_t$は時刻$t$におけるデータ、$S_t$は季節成分、$T_t$はトレンドとサイクルを合わせた成分(これ以降は単にトレンド成分と呼ぶ)、$R_t$は残差成分を表しています。
時系列データを各要素に分解することで、興味に基づいた最適なデータを取得することが可能になります。例えば、失業データでは一般的に季節調整データと呼ばれる時系列データから季節成分を取り除いたデータ$y_t-S_t$が使われます。これは、一般的に失業データを見る際には、景気後退のような季節によらない変動のみに関心があるためです。その他にも、傾向の変化に関心があるのであれば、トレンド成分$T_t$を見るなど、要素に分解することで最適な観測が行えるようになります。ここからは、各要素に分解するための手法について見ていきます。
古典的分解
古典的でシンプルな手法です。各要素は以下の3ステップから求められます。
Step1: 移動平均を用いて時系列データからトレンド成分$\hat{T_t}$を抽出する
Step2: 時系列データからトレンド成分を取り除いたデータ$y_t-\hat{T_t}$に対して、すべての季節の平均を取り、季節成分$\hat{S_t}$を取得する
Step3: $y_t-\hat{T_t}-\hat{S_t}$を計算し、残差成分$\hat{R_t}$とする。
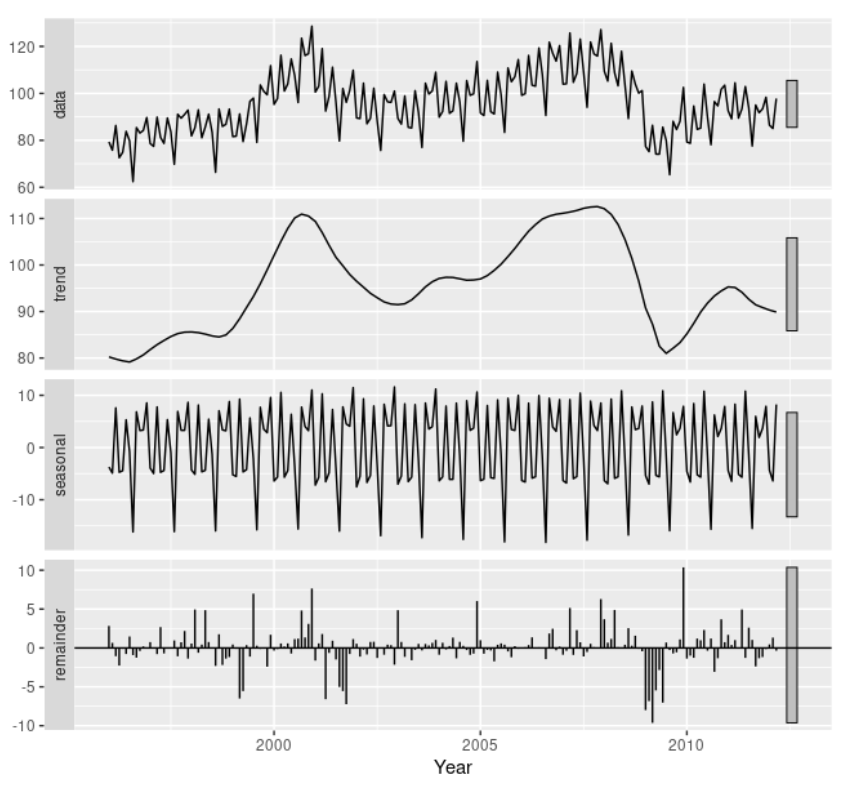
古典的分解手法では、移動平均によりトレンドを求めているため、最初と最後の一部の要素を求めることができません。また、トレンドがなめらかになりすぎることにより、残差にトレンドが残ってしまうといった問題やどんな波形に対しても季節成分が平均化されてしまうといった問題などがあります。
ヨーロッパでの電子機器の注文数のデータに対しての例を見ていきます。
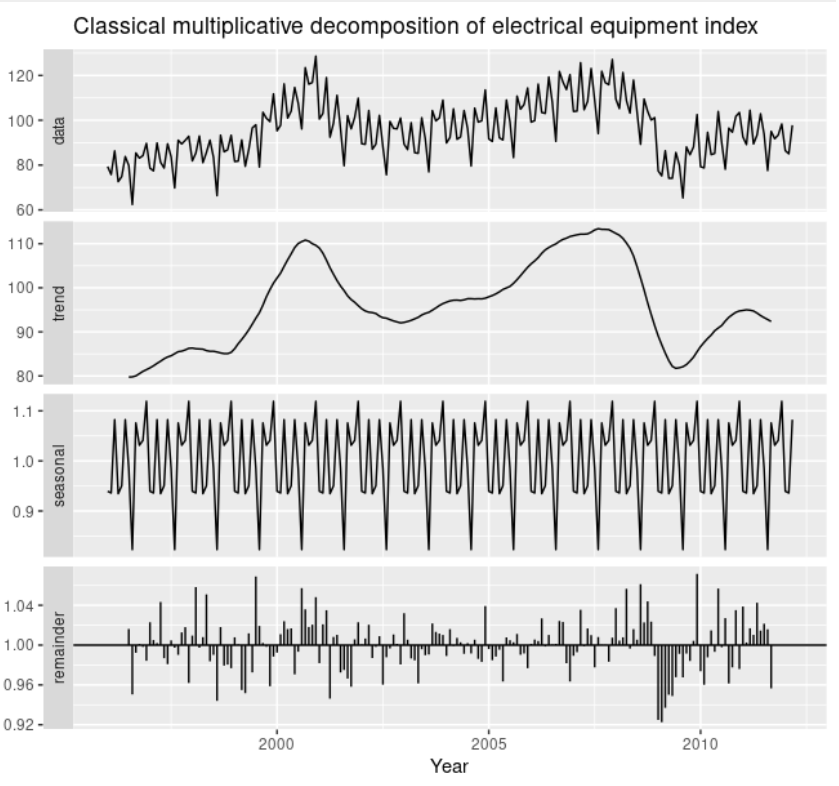
X11分解
X11は古典的分解手法を発展させた手法です。この手法では、すべてのデータに対してトレンドを求めることができます。さらに、季節成分が時間によって少しずつ変化することが可能になっています。先ほどと同様の例を見てみると、トレンドの急激な下降をよくとらえています。
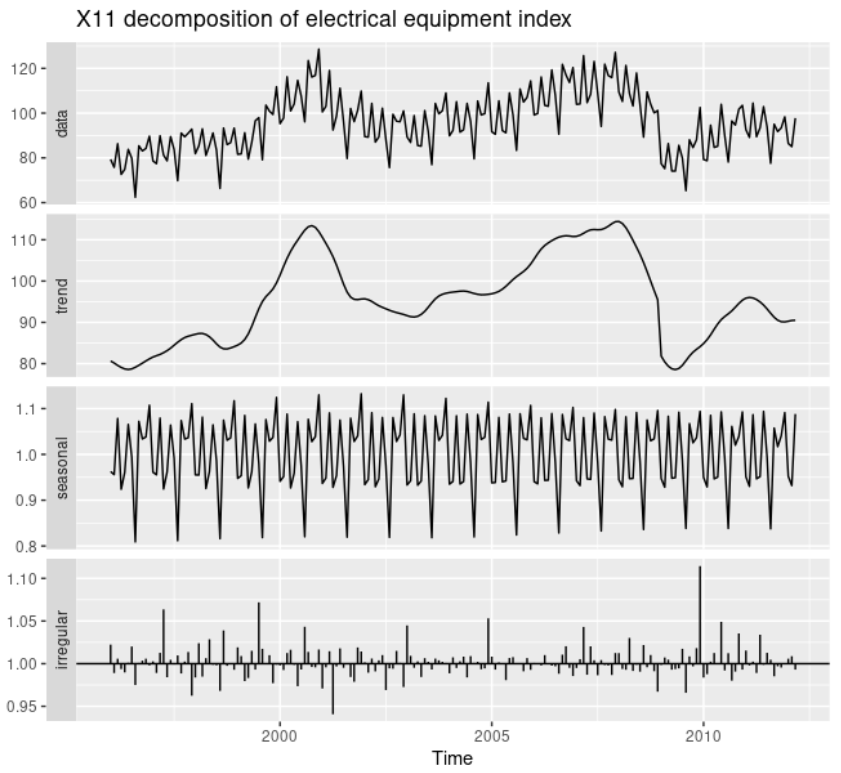
SEATS分解
SEATSはARIMAを利用したモデルです。この手法は四半期あるいは月次データにのみ利用可能です。
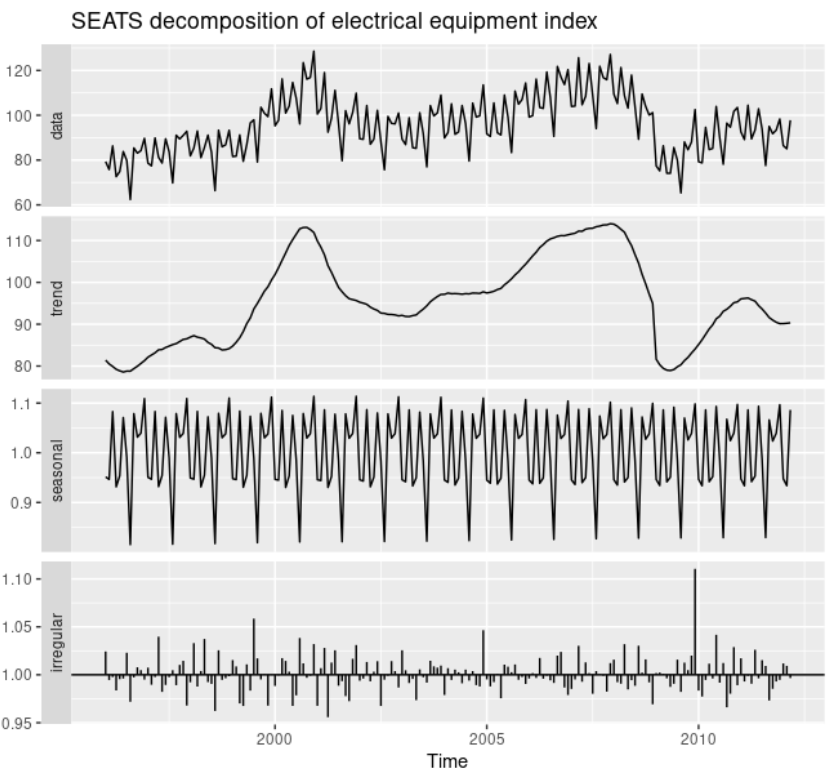
STL分解
STLはロバストな手法です。どんなタイプの季節性に対しても利用することができます。また、季節成分が時間によって変化することができます。