今回は、「因果探索」と呼ばれる分野に共通する基本的な考え方についてまとめてみました。
そもそも因果探索って？
因果探索は、「データを用いて因果グラフを推測すること」です。「因果関係を発見するための手法」とも言えるでしょう。
では、因果関係は？
因果関係は、「一方が変化することにより、それに伴ってもう一方にも変化が及ぶ関係」と表現できると思います。この関係が示されることにより、目的を果たすためには何に対して働きかけるべきなのかがわかります。
因果を考えるうえで欠かせないのが、相関との区別でしょう。相関は「一方の値に応じてもう一方の値に傾向がある関係」と考えます。決定的な差は、2つの要素をつなぐ線が有向か無向かということでしょう。因果は伴った変化であることから、一方からもう一方への矢印が明確に存在します。対して、相関は傾向ですので、2つの要素をつなぐことはできたとしても、矢印までは確定できません。
因果探索は、要素のつながりを矢印で表現するための手法とも言えるでしょう。
どうやって因果を探索するの？
先述の通り、因果探索は「データを用いて因果グラフを推測すること」です。この実現は、因果グラフの仮定→データとの矛盾の有無の確認という流れで行われます。
因果グラフの仮定
要素Aと要素Bの関係は、
- A→B（原因：要素A、結果：要素B）
- B→A（原因：要素B、結果：要素A）
- A↔B（双方向の因果）
- 無関係（直接的な関係なし）
の4つに大別できます。各要素の関係を4つから仮定することで、因果グラフの仮定は完了します。
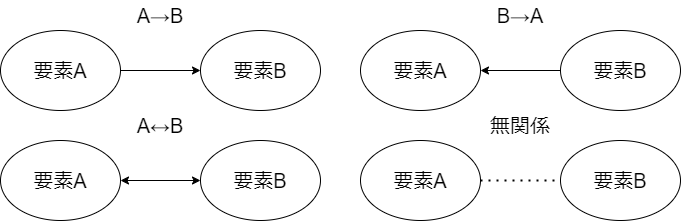図1．2つの要素間の因果関係のパターンデータとの矛盾の有無の確認
仮定した因果グラフより、各要素の値を構造方程式により表すことが可能になります。
構造方程式は以下の要素で構成されます。
- 内生変数
式で定義したい対象の変数。下の例では、要素Aや要素Bの値が該当する。 - 外生変数
構造方程式の右辺にのみ現れる。誤差や未観測の要素を含めて設定する。 - 関数
値の写像に用いる。下の例では、Bを算出するためにAとeBを変数とした関数を設定した。 - 外生変数の確率分布
構造方程式内で定義されない外生変数に関する設定。今回は詳細は割愛します。
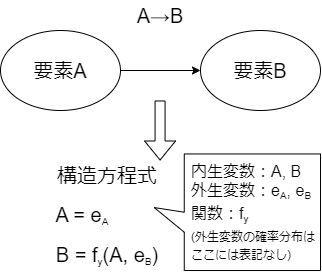図2．要素A→要素Bという因果関係を仮定したときの構造方程式の例これにより、要素Aと要素Bに対応する値が算出可能になり、実データが示す値と因果モデルから算出される予測値を比較することができます。これにより、仮定した因果グラフの妥当性が導かれ、因果グラフの推測が完了します。
基本的な流れは以上になります。ただ、未知数が多すぎるためこれを単純に解くことは難しいです。後述しますが、この問題を解くためにはこの先の世界にさらに足を踏み入れる必要があります。
どんなことに活かせる？
施策等の改善
ビジネスシーンでは、売上の増加、解約率の減少、契約率の増加といった利益に直結する様々なターゲットが存在します。ターゲットと因果関係のある数値や施策を見つけることができれば、それを変化させることでターゲットの変化も見込めます。何もわからない状態で闇雲に施策の実施や変更をするよりも、効率的かつ効果的に結果を得ることが可能だと考えられます。
その他にも…
因果探索を使えばこんな課題が解決できそう、と感じた方はぜひお話を聞かせてください。
最後に
ここまで因果探索における基本的な考え方を書かせていただきました。現状の私の理解ですとこのような表現になります。「ここが違う」というようなことがあれば、ご指摘いただけると嬉しいです。
また、本記事の最初でも少し述べましたが、参考にした書籍『統計的因果探索』の前半部分にしか触れておらず、今回の内容は因果探索の入口を覗いたにすぎません。この先の果てしない世界については、別の機会に触れたいと思います。
