5.対応分析(コレスポンデンス・アナリシス)
はじめに
データ行列の、(基本的には)行要素同士/列要素同士の距離関係を図示します。ポアソン分布する値の行列を標準化して特異値分解します。
ちなみに……
この手法は,数量化Ⅲ類(パタン分類の数量化)と、数学的には同等です。ただし、標準的には同じデータを分析したら同じ数字が出てくるのではありません。
また両者は、必ずしも同じ目的で作られたものではありません。同等の手法として使えますが、各手法の生み出される筋道は、林知己夫(以下、人名は敬称略)のパタン分類の数量化(数量化Ⅲ類)とベンゼクリのコレスポンデンスアナリシス(対応分析)とでは異なります。
どうも、両者は混同されているように感じます。ここでは対応分析(コレスポンデンスアナリシス)を扱います。
なお「数量化○類」という呼称は、飽戸弘によるものです。林知己夫本人も、この呼称をしばしば使ってはいましたが、林知己夫本人による命名ではありません。
対応分析の計算手続(ポアソン分布する値の標準化)
対応分析では、標準的には分割表(N表)を解析対象とします。ここではSA(シングル・アンサー:単一回答)のクロス集計表(分割表)を考えます。MA(マルチプル・アンサー:多重回答)の場合は、多重対応分析となり、また少し様子が異なってきます。ここでは扱いません。
以下、標準的な筋道での説明とは異なりますが、実測値を、ポアソン分布する値として、行と列を同時に標準化して、特位値分解する、という筋道で説明します。こうすると、値が正規分布する場合も同様の手続きで計算できるので(たとえば平均値表)、汎用性が出ます。
さて、分割表ですが、たとえば、下記(図表1)のようなものです。
図表1.分割表ここで各セルの値はポアソン分布すると考えます。そうすると、平均も分散も行和や列和で求められます。具体的に以下で見ていきます。
さて、あらためて図表1.の小計/合計部分を除いた度数表部分だけを行列で書くと、図表2.の通り。
 図表2.度数表(実測値行列)
図表2.度数表(実測値行列)この行列をもとに計算していきます。ちなみに総計(全体)は861です。
図表2.の行列について、行和を計算してみます。
 図表3.行和
図表3.行和同様に列和をとると、図表4.の通り。
これらを使って、期待値行列を計算します。これは、行和、列和、総計を使って求めます。これは、各セル(各成分)について、

で求められます。具体的に図表2.の行列について期待値行列を計算すると、図表5.の通り。
 図表5.期待値行列
図表5.期待値行列セルごとに実測値から期待値を引く(Ⅲ類で、固有値分解後の第一次元を捨てるのに相当)と、残差が求まります。
 図表6.残差行列
図表6.残差行列ここで、行和(図表3)と列和(図表4)から、行や列の標準偏差を計算します。これは単純に、
![]()
で求まります。ポアソン分布の場合、単純に合計を、平均としても分散としても用います。なので、行や列の標準偏差は、
![]()
あるいは
![]()
で求められます。後の都合もあり、以下ではそれぞれの逆数の対角行列で表しておきます。
 図表7.行の標準偏差の逆数の対角行列
図表7.行の標準偏差の逆数の対角行列 図表8.列の標準偏差の逆数の対角行列
図表8.列の標準偏差の逆数の対角行列さて、ややこしい話が続きましたが、<図表7の行列(行の標準偏差の逆数の対角行列)× 図表6の行列(残差行列)× 図表8(列の標準偏差の逆数の対角行列)の行列>によって、行と列について同時に標準化した、残差行列(平均からの偏差を、標準偏差で除した値)を計算します(図表9)。対応分析は、この行列(図表9.標準化した残差行列)を特異値分解することで解けます。
 図表9.標準化した残差行列
図表9.標準化した残差行列行のスコア/列のスコア
図表9.の行列を特異値分解すると、特異値と(左/右)特異ベクトルが求まります。得られた(左/右)特異ベクトルから、列和/行和の割合の平方根の逆数の対角行列と、特異値の対角行列を使って、行/列のスコアを計算します(計算過程省略)。
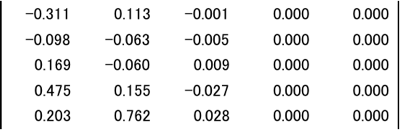 図表10.列のスコア
図表10.列のスコア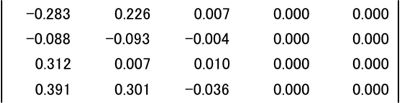 図表11.行のスコア
図表11.行のスコア絶対寄与と相対寄与(平方相関)
対応分析でとても有用なのが、絶対寄与と相対寄与です。スコアの計算にあたっては、行要素/列要素ともその分散を揃えて(標準化して)計算(特異値分解)しました。絶対寄与/相対寄与の計算は、特異ベクトルに周辺度数をかけて、分散の大きさを戻して行います。
絶対寄与は、その軸では、どの要素に着目すればよいか(どの要素は気にしなくて良いか)を軸ごとに割合で示します。行要素/列要素ごと、各軸分を足し合わせると100%になっています。
絶対寄与は以下の通り。

 図表12.絶対寄与
図表12.絶対寄与
※上5行が列要素、下4行が行要素
相対寄与は、その要素では、どの軸に着目すればよいか(どの軸は気にしなくて良いか)を要素ごとに割合で示します(100をかければ%)。行要素/列要素とも、要素ごとにすべての軸を足し合わせると、1になっています。
相対寄与は以下の通り。
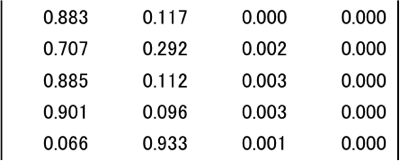
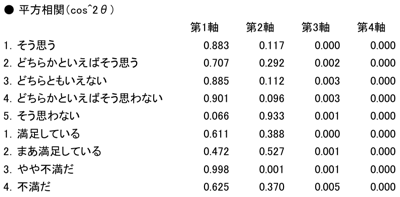
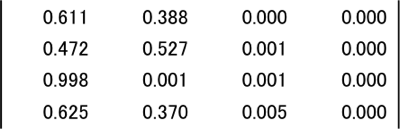 図表13.相対寄与(平方相関)
図表13.相対寄与(平方相関)
※上5行が列要素、下4行が行要素
また、対応分析では、行と列の相関は必ず1を切ります(行要素と列要素は次元を共有しない)。もし、行と列の同時付置をする場合でも、次元間の相関があまり大きくない場合は、無視する(結果を見ない)ほうが良いかもしれません。あるいは見るとしても、次元間の相関は、1軸から順に小さくなっていくので、最低限(1軸×2軸)しか見ないほうが良いかもしれません。(理屈上は行と列は同時付置すべきではありません。ですが経験上はしばしば同時付置も行われています。本連載の例は同時付置です。)
解釈
図表1.の分割表を対応分析した結果は、通常、以下のようになると思います。
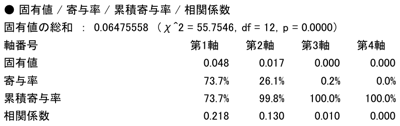
図表14.固有値ほか
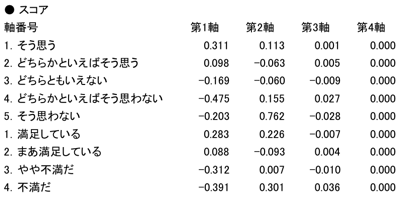
図表15.軸のスコア
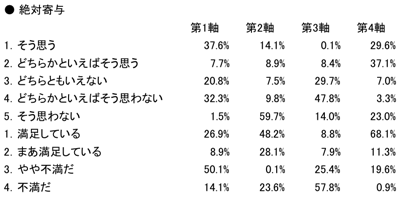
図表16.絶対寄与
図表17.相対寄与
スコアを使って、行要素と列要素を同時付置すると、図表18.の通り。同時付置は理屈としては「誤り」ですが、ここでは相対的に両要素間の相関が高い、1軸と2軸だけを使って行っています。
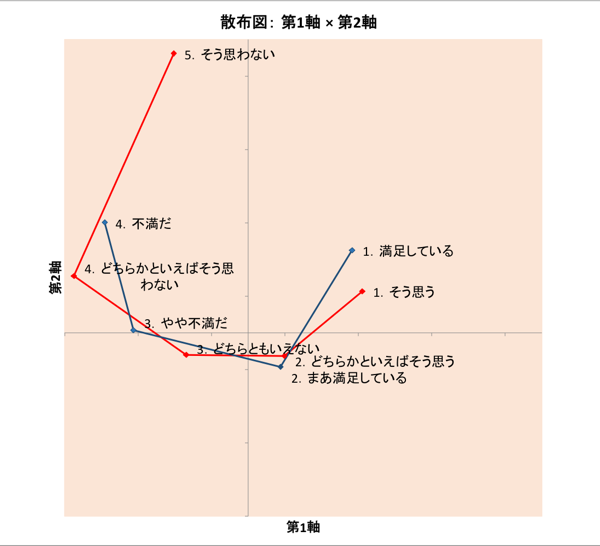 図表18.散布図(1軸×2軸)
図表18.散布図(1軸×2軸)Q1-5(赤線)、Q7(青線)とも、順序尺度となっているため、恐らく「馬蹄形問題」が起きているのでしょう。意味内容から考えても、2軸目の寄与率が26.1%とあまり大きくないことからしても、軸に名前を付ける意味もないでしょう。単純に、「生活満足度が高いことと、学生同士の仲が良いと思っていることとは、強く関係している」といった解釈で良いのではないのでしょうか。
なお、どちらの質問も(行要素も列要素も)、「2」「3」が原点近くに付置されています。逆に、Q1-5の「5」という点は、原点から離れて付置されています。これは、特異値分解する前の行列を作るとき、各セルとも、行、列の分散(行和、列和)で割っている(逆数の行列をかけている、標準化している)からです(度数の多い要素は大きな数字で割る=値が小さくなる=原点(0)に近づく)。
同様に(反対に)、行和あるいは列和が小さいことは、標準偏差(分散)が小さいことになります。値の標準化では、小さな値で割ります(結果、大きな値となります=原点(0)から遠ざかります)。