『データ分析になぜ統計学が必要か』シリーズのPart1, Part2 では、統計学でできることや統計分析の特徴を説明しました。
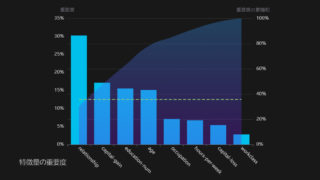
先述の通り、統計分析は、ビジネス、社会、学術界のさまざまな場面で活用されています。データ分析の基礎となる統計分析の手法を使いこなすことがデータサイエンティストにとって強力な武器です。
今回は、さまざまな分析手法の中から、統計学に基づいた分析(統計分析)の手法や事例をいくつか紹介します。
あらゆる場面で行われる統計分析
統計分析というと、Excelを用いた分析を思い浮かぶ方が一定数いますが、ここで紹介する分析はツール(Excel、Python、BIツールなど)によらず、統計学にもとづいて行うことができます。
例えば、Python言語で記述したデータ分析のプログラムでは、データを読み込み、専用のライブラリや関数を使えば、簡単なコーディングでデータに処理を施すことができます。例えば、データを度数分布表もしくはヒストグラムとして表示し、さらに内訳表示や平均値のリファレンスラインを入れたりすることができます。これらは統計分析に含まれる度数分析やデータ分布の観察として捉えることができます。
統計分析の例1:度数分析
統計分析では、データの分布やばらつきを視覚的に把握・理解するために、目的に合ったグラフや表で可視化することがあります。その1つが度数分布表とヒストグラムです。
度数分析では、データの数値をいくつかの階層に分け、各階層に属するデータの個数を表示することでデータを整理します。これによって「度数分布表」が得られます(図1)。
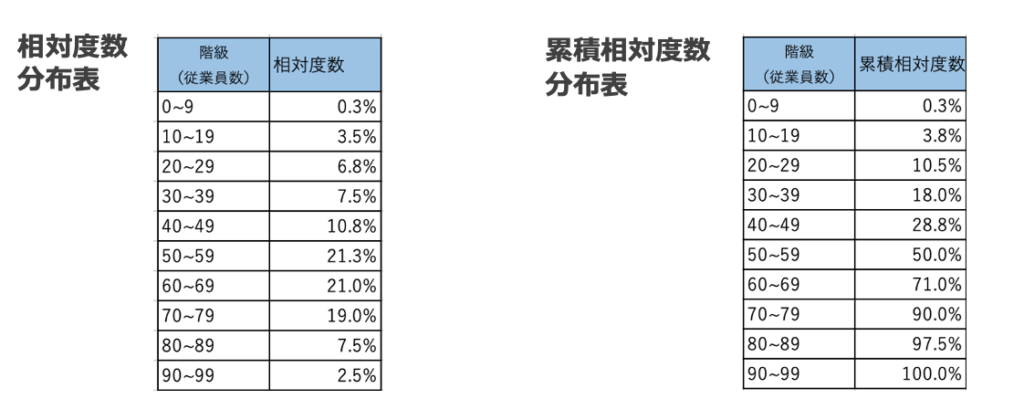
図1 :度数分布表の一種である相対度数分布表(左)と累積相対度数分布表(右)
度数分布表を棒グラフ状にプロットしたものを「ヒストグラム」と呼びます(図2)。数値の表である度数分布表をグラフに変換することで、データが代表する母集団の分布や傾向を直感的に把握しやすくなります。
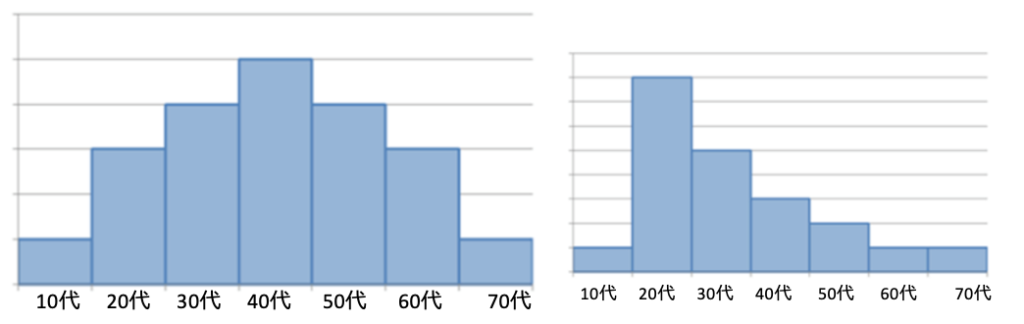
図2:社員の年齢のヒストグラム・左側の企業では、30~50代が多い。右側の企業では20代に偏っている「若い会社」。
図2のヒストグラムのような「左と右の広がりが違う」分布をしていると、なぜこの偏りが発生しているのかを考えさせられ、課題の解決につながります。このように、データの可視化を通じて、データの広がりを知ることでアクションにつながる示唆が得られます。
度数分析の用途例を1つ挙げましょう。
ある企業の主力商品カテゴリーA,B,Cについて、カテゴリーごとに売上の平均を算出したところ、カテゴリーBがAとCより目立って平均が高かったのです。
この場合、販促予算をすべてカテゴリーBの商品に割り当てようとすぐに決めてはいけません。各カテゴリーの売り上げの分布を見る必要があります。結果としてカテゴリーBには非常に高額な商品が1つあり、この商品が数回売れただけで、全体の平均を押し上げている可能性があります。これに対して、もしもカテゴリーAとCが安定に売上をあげ続けているのであれば、将来的な見込みとしてカテゴリーA、Cの方が有望で営業に力を入れたくなります。
これは、平均値だけに惑わされてはよくない、データの分布を見ることも重要であることを主張する例です。
統計分析の例2:回帰分析
統計分析の中で、最もよく使われている手法の1つは回帰分析です。回帰分析では、分析・予測の結果に相当する「目的変数」とその変動に寄与する「説明変数」の関係を解明することを目指します。
説明変数と目的変数の関係性を捉えた数式は「回帰式」または「回帰モデル」と呼びます。図3におけるデータ点に当てはめられている直線が回帰式です。
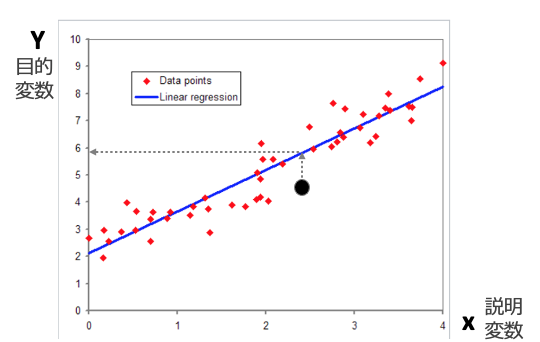
図3:説明変数Xを用いて目的変数Yを回帰で求める回帰分析の例
いったん回帰式を求めることができれば、それを将来のデータに対する予測に使えます。つまり、回帰式に当てはめることで、現時点でまだデータがない領域の値を予言できます。
将来予測だけではなく、常にそうとは限らないですが、説明変数と目的変数の間に「原因と結果」の関係が存在することがあるので、この関係を探索することで、現状の理解や改善、課題の発見と解決につながることが可能です。例えば、横軸に商品Aの販売数、縦軸に関連商品である商品Bの販売数をとると、商品Aが売れれば売れるほど商品Bが売れる可能性がある、という要因の分析につながります。
統計分析の例3:クラスター分析
「クラスター分析」とは、さまざまな変数(特徴量)を持つデータが混ざり合った集団の中から、互いに類似点を持つデータ同士を集めてグループ分けする統計的な分析手法です。言い換えると、データに含まれる特定の特徴量を軸に比べた際に、データ同士が「似ているか」、または「似ていないか」を基準にデータを整理します。類似度(非類似度)はデータ点の間の距離を計算することで求めます。
クラスター分析は、高度な統計手法の一種である「多変量解析」に属します。多変量解析は、値の予測に使われることもあり、クラスター分析のように、データの中の数々の変数を集約し整理することで「要約」することにも使われます。
クラスター分析の人気な用途の1つは「顧客セグメンテーション」です。会員登録データ、購買データ、アンケートデータなどを用いて「どのような顧客層がいるのか」を認識することを目指した分析です。どのような種類の顧客が存在するかを推測し、その情報をもとに、ブランドポジションの確認や顧客セグメントごとの効果的な販促(クーポンやキャンペーン)を打ち出すことができます。顧客だけではなく、たとえば商品についても、クラスターごとの特性を分析できます。そうすると、それぞれのクラスター(データ群)に最適な施策を打てやすくなります。
上記の例のように、膨大なマーケティングのデータがあり、このデータに含まれる項目のうち、どれをグループ分けの基準にすれば良いのかが一眼でわからない場合にクラスター分析が効果的です。















