こんにちは。分析官のA.K.です。今回はTableau上で傾向線を再現する方法を解説していきたいと思います。
前編では、傾向線の計算式についての解説をし、後編では、実際にTableauで再現する方法を解説していきたいと思います。
アナリティクス機能を使用した傾向線
Tableauには標準でアナリティクス機能が備わっており、これを使用することで簡単に傾向線が引くことが可能です。
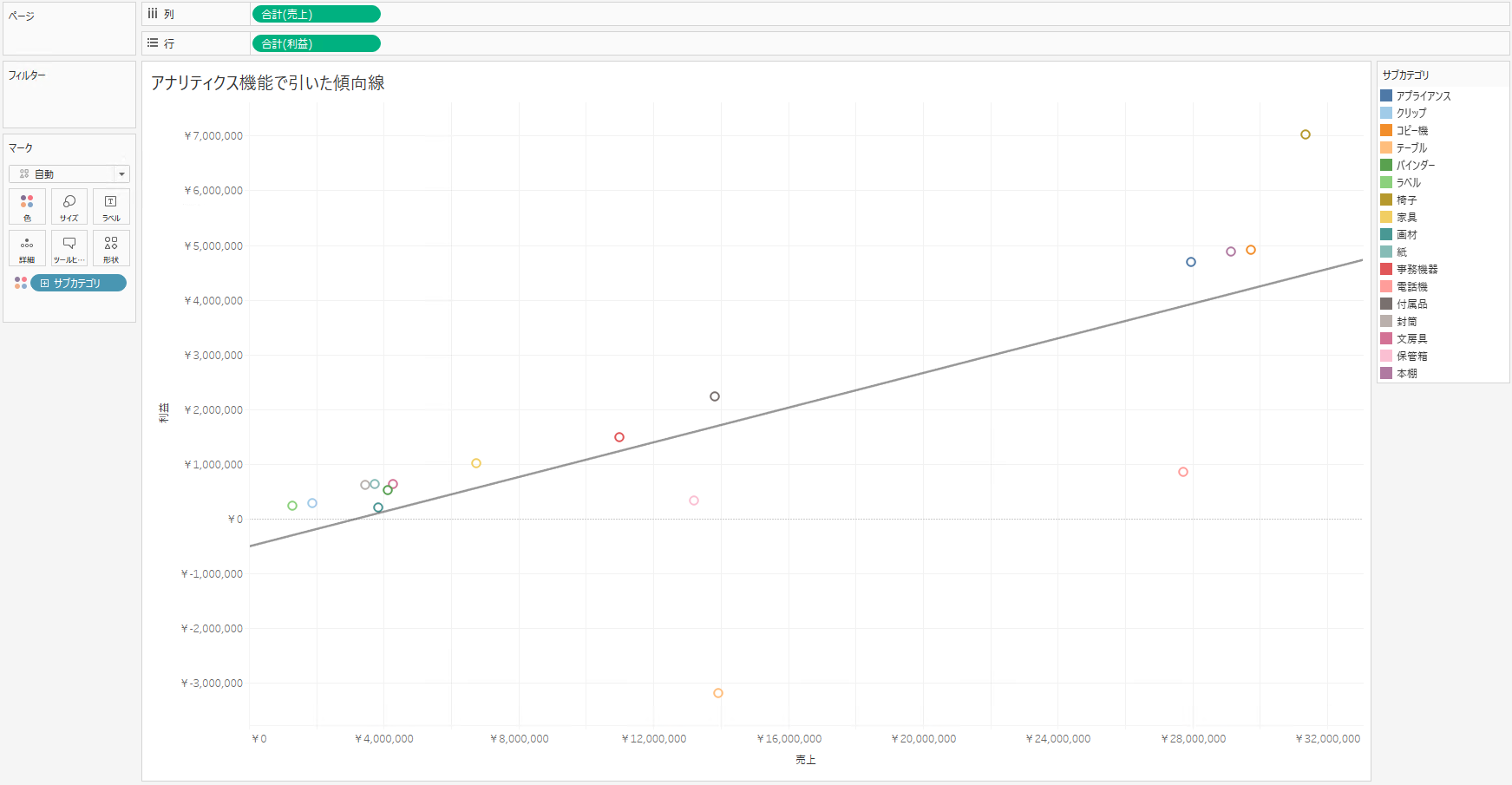
またカスタマイズをすることで、単回帰直線だけでなく、多項式の曲線や対数曲線を引くことも可能です。
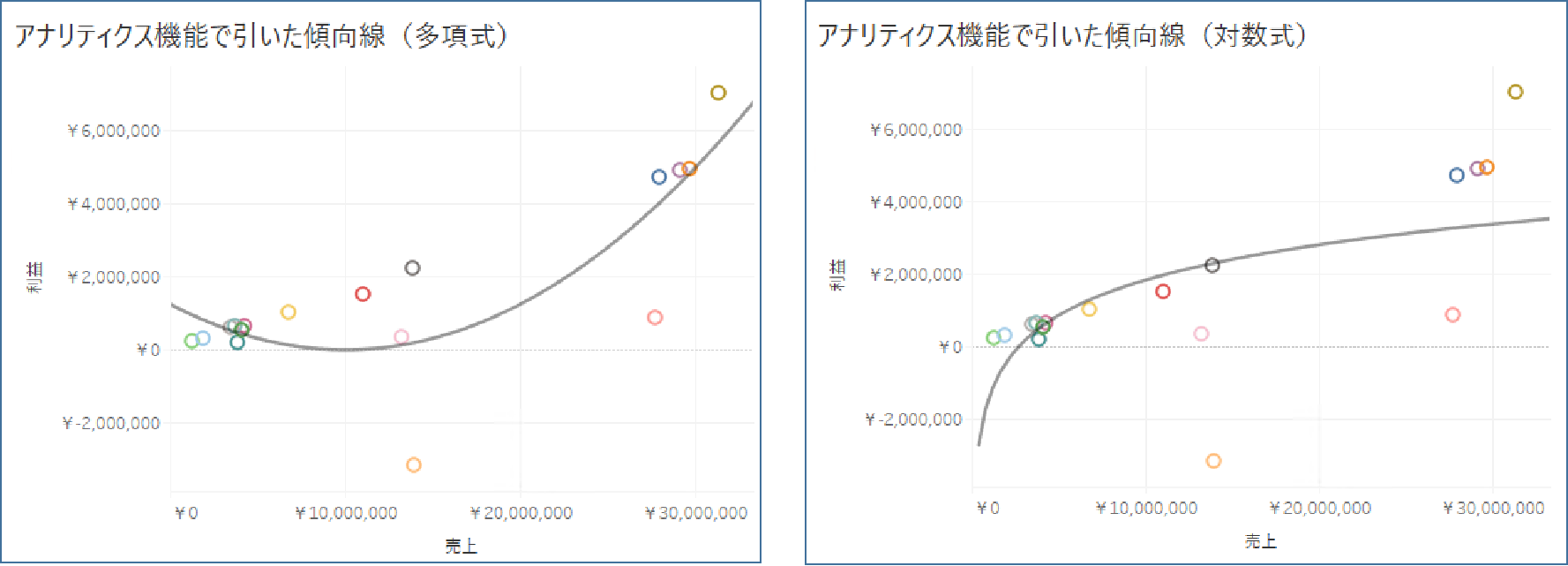
アナリティクス機能の傾向線は非常に手軽かつ便利で、分析をするだけであればシート上にサクッと反映させて分布の傾向や外れ値を理解する際に役に立ちます。
ただ、一方で物足りない場面もあり、シート上で引かれている傾向線の係数を使用して別の計算やデータの予測値を算出させる、といったようなことができません。
そんな傾向線を手動で作成することで、傾向線の係数を自由に使えるようにしてみたいと思います。今回は一番簡単で使用頻度が高いと思われる単回帰直線を対象に解説していきたいと思います。
単回帰直線の計算式の解説
まず単回帰直線をTableau上で作っていく前に、単回帰直線の計算式について少しだけ解説しようかと思います。
単回帰直線は下記式で表される線になります。

中学校とかで習う比例の式ですね。この時、yはグラフの縦軸に該当する値、xはグラフの横軸に該当する値になります。
すなわち、単回帰直線をTableau上で表現するためには、傾きaの値と切片bの値を計算することが出来れば単回帰直線を引くことが可能になります。
傾きaの導出
単回帰直線において、傾きaの式は下記の式で定義されています。
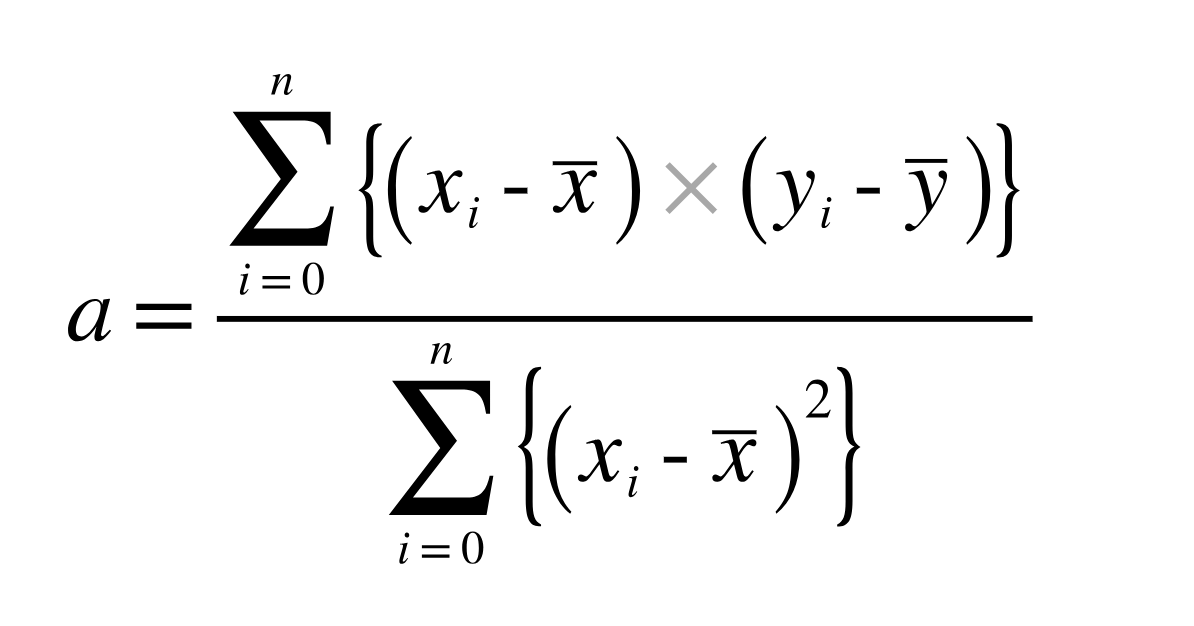
数学恐怖症の方からすると、上の式だけ見ると非常にいかつくて「無理」ってなってしまうかなと思います。(自分も結構、無理な人です。)
ただ中身を言葉に変換してみると非常にシンプルで、分子はXとYの共分散で、分母はXの分散です。すなわち、単回帰直線の傾きaはXYの共分散をXの分散で割った値になります。
切片bの導出
切片bの式は下記の式で定義されています。
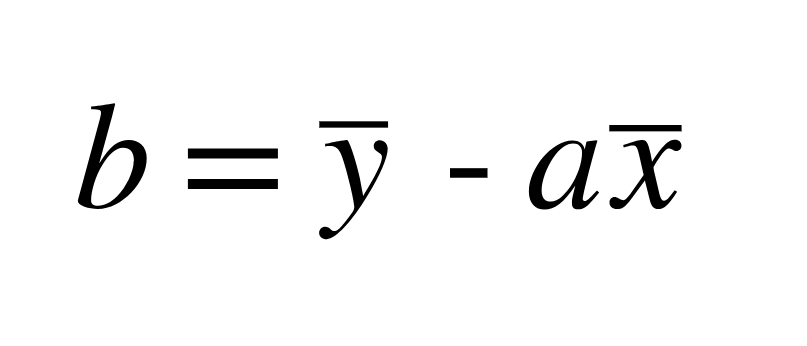
xやyの上に横線が引いてある記号は平均を表すマークで、「Xバー」とか「Yバー」と読みます。こちらは比較的簡単ですね。切片bを導出するためには、yの平均値から(傾きa)×(xの平均値)をした値を引けば良いわけです。
単回帰直線を引くために必要な値
以上のことをまとめると、下記の値をTableauで算出できれば傾向線が引けるようになります。
- 傾きaに必要な値
- XとYの共分散
- Xの分散
- 切片bに必要な値
- 傾きaの値
- Xの平均値
- Yの平均値
次回は実際にTableauを使用して、単回帰直線を引く方法を解説していきたいと思います。
















